Multi-View Geometry 및 Camera parameter 개념 정리
다크 프로그래머님의 [영상 Geometry] 블로그 글을 읽고 요약 정리한 내용입니다. 이번 포스트의 내용은 모두 해당 블로그 글을 기반으로 합니다.
1. 좌표계

1.1. 월드 좌표계 (World Coordinate System)
- 사물(물체)의 위치를 표현할 때 기준으로 삼는 좌표계
- 절대적인 좌표계가 아님. 우리가 임의로 잡아서 사용가능한 좌표계
- e.g. 방 한쪽 모서리 = 원점일 때, 한쪽 벽면 방향 = X축, 다른쪽 벽면 방향 = Y축, 하늘 바라보는 방향 = Z축
- 월드 좌표계 상의 점 표기: P(X,Y,Z)

1.2. 카메라 좌표계 (Camera Coordinate System)
- 월드 좌표계: 우리가 살고 있는 공간의 한 지점을 기준으로 한 좌표계
- 카메라 좌표계: 그와 달리, '카메라'를 기준으로 한 좌표계, 길이 단위는 월드와 카메라 좌표계가 동일해야함 (mm 등)
- 카메라의 초첨 (렌즈 중심) = 원점, 카메라 오른쪽 방향 = X축, 카메라 아래쪽 방향 = Y축, 정면 광학축 방향 = Z축
- 카메라 좌표계 상의 점 표기: Pc(Xc,Yc,Zc)
1.3. 픽셀 (이미지) 좌표계 (Pixel (Image) Coordinate System)
- 우리가 실제 눈으로 보는 좌표계
- 이미지 왼쪽 상단 (left-top) 모서리 = 원점, 오른쪽 방향 = x축 증가 방향, 왼쪽 방향 = y축 증가 방향
- 픽셀 좌표계의 x, y축에 의해 결정되는 평면 = 이미지 평면 (image plane)
- 픽셀 좌표계 상의 점 표기: p_img(x,y)
- 3D 공간 상의 한 점 P = (X,Y,Z)는 카메라의 초점 (렌즈 초점) 을 지나, 이미지 평면 상의 한 점 p_img = (x,y)에 투영됨
- 점 P와 점 p_img를 잇는 ray 상의 모든 3D 점들은 모두 p_img로 투영됨
- 따라서 3D 점 P로부터 p_img는 유일하게 결정됨. 그러나 p_img로부터 3D 점 P를 구하는 것은 부가 정보 없이 불가능
1.4. 정규 좌표계 (Normalized Image Coordinate System)
- 편의상 도입한 가상 좌표계
- 카메라의 내부 파라미터 (intrinsic parameter) 의 영향을 제거한 이미지 좌표계
- 좌표계의 단위를 없앤, 정규화된 좌표계이며, 카메라 초점과의 거리가 1인 가상의 이미지 평면을 정의하는 좌표계
- 정규 이미지 평면의 중점 (광학축 Zc와의 교점) = 원점 → 픽셀 좌표계와 원점의 위치가 다름
- 정규 좌표계 상의 점 표기: p'(u,v)

- 내부 파라미터 행렬 K를 알면 픽셀 좌표와 정규 좌표 사이의 변환 가능 → p_img = Kp'
- fx, fy = 초점 거리, cx, cy = 주점 (광학축과 영상 평면이 만나는 픽셀 좌표) 일 때, 위 수식이 성립함.
- 가운데의 3x3 행렬 = 카메라 행렬 (camera matrix) K
- x = fx * u + cx, y = fy * v + cy (픽셀 좌표 계산)
- u = (x - cx) / fx, v = (y - cy) / fy (정규 좌표 계산)
- 정규 이미지 평면과 정규 좌표계 도입 이유?
→ 동일 장면을 동일 위치, 각도에서 찍더라도 서로 다른 카메라 특성, 세팅에 따라 서로 다른 영상 얻음
→ 일관된 기하학적 해석을 위해선 카메라 차이 없어야 함
→ 카메라 차이라는 요소를 제거한, 정규화된 이미지 평면에서 공통된 기하학적 특성을 분석하고 이론 수립하는게 효과적
* Camera param.은 월드 좌표계의 3D 복셀 좌표를 카메라 좌표계를 거쳐, 픽셀 좌표계의 2D 픽셀 좌표로 변환하는 파라미터. Extrinsic param. [R|t] 와 Intrinsic param. K 의 행렬곱 P 로 이루어짐.

* Extrinsic param.은 3D 공간에서 카메라가 어디에 위치하고 (3D Translation) 어디를 바라보는지 (3D Rotation) 나타냄. 월드 좌표계 → 카메라 좌표계로 변환시켜주는 파라미터
* Intrinsic param.은 초점 거리 (fx, fy), 주점 (cx, cy), 비대칭 계수 (skew) 등 카메라 렌즈와 센서 위치에 의해 결정됨. 이미지 패널이 얼마나 이동 (2D Translation)하고, 얼마나 확대되고 (2D Scaling), 얼마나 기울어졌는지(2D Shear) 나타냄. 카메라 좌표계 → 이미지 좌표계 로 변환시켜주는 파라미터
2. Homogeneous Coordinates
2.1. Homogeneous Coordinates
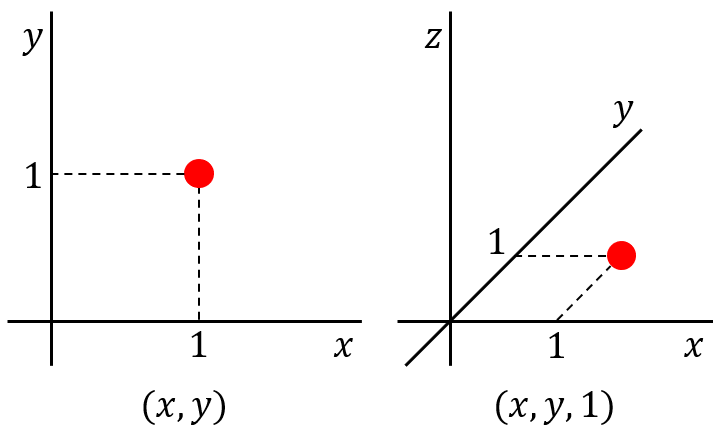
- 쉽게 말하면 위 그림처럼 좌표 (x,y)를 (x,y,1)로 표현하는 것
- 공식적으론 w = 0이 아닌 상수일 때, (x,y)를 (wx,wy,w)로 표현하는 것, 3차원에선 (X,Y,Z) → (wX,wY,wZ,w)
- 즉, Homogeneous Coordinates에서 scale은 무시되며, (x,y)에 대한 homogeneous 좌표 표현은 무한히 존재함
- homogeneous 좌표에서 원래 좌표 구하기: 끝자리가 1이 되도록 scale 바꾼 후 1 떼내기
- e.g. (x,y,a) → (x/a,y/a,1) → 실제 2D 좌표: (x/a,y/a)
- 컴퓨터 그래픽스 또는 3D 비전에서 Homogeneous Coordinates 많이 활용
→ affine 변환이나 perspective (projective) 변환을 하나의 단일 (single) 행렬로 표현할 수 있기 때문
- 사영 기하학 (projective geometry) 에서 사용하는 좌표가 homogeneous 좌표이며 이를 projective 좌표라고도 함
- homogeneous 좌표가 투영 (projection)과 무슨 관계가 있길래 사영 기하학과 함께 나오나?
- 우리가 보는 카메라 영상은 3차원 공간에 있는 점들을 이미지 평면에 투영시킨 것
- 카메라 초점과 투영된 점을 연결하면 하나의 긴 투영선 (projection ray) 이 나옴
- 그런데, 이 선 상에 있는 모든 점들은 모두 동일한 한 점으로 투영됨
- 그렇다면, 이미지 평면상의 한 점에 대한 homogeneous 좌표라는 것은 이 점으로 투영되는, ray 상의 모든 점들을 한꺼번에 표현하는 방법인가?
- 정규 이미지 평면 (normalized image plane) 상의 한 점 p' = (u, v) 에 대해 생각해보자.
- 그림1에서, 점 p' = (u, v)에 대한 homogeneous 좌표 표현은 (u, v, 1) 임
- 그런데, 점 p'을 카메라 좌표계로 봤을 때의 3D 좌표도 (u, v, 1) 임
- 카메라 좌표계 입장에서 보면 투영선 상에 있는 점들의 3D 좌표는 일반적으로 w(u, v, 1) = (wu, wv, w)가 됨
- 그런데, 이것은 (u, v)의 일반적인 homogeneous 좌표 표현과 정확히 일치함
∴ homogeneous 좌표 자체가 이 점으로 투영되는 ray 상의 모든 점을 한꺼번에 표현하는게 맞고,
그래서 homogeneous 좌표를 projective 좌표라고도 함.
2.2 사영 기하학(projective geometry)
- 사영기하학: 투영 변환 (projective transformations) 에 대해 불변인 기하학적인 특성을 연구하는 것