활성화 함수(Activation function) 설명 (Sigmoid, ReLU, LeakyReLU, tanh)
# 왜 활성화 함수를 사용하는가?
모델의 비선형성을 증가시키기 위해. 비선형성이 증가하면 기존 특징 공간이 더 좋은 특징 공간으로 변환되어 선형 분류가 쉬워진다.
# 알고 있는 Activation function에 대해 알려주세요.
* Sigmoid 함수 ( = logistic 함수)

입력 신호들을 받아 선형 결합을 해서 만들어진 값에 hard threshold를 적용했던 Step function (계단 함수) 이 있다. 하지만 해당 함수는 미분이 불가능하기 때문에 딥러닝에서 역전파를 수행할 수 없다. 이를 해결하기 위해서 제안된, 부드러운 형태의 미분 가능한 함수가 sigmoid함수다.
sigmoid 함수는 -inf~+inf 값을 0~1 사이의 값으로 매핑해줌. 입력값 x가 양수면 0.5보다 큰 값, x가 음수면 0.5보다 작은 값을 뱉는 활성화 함수. 따라서 threshold 0.5를 기준으로 이진 분류 문제에 많이 쓰인다(binary classifier). 한편 x가 매우 큰 값일땐 1, 매우 작은 값일땐 0을 뱉어낸다. 여기서 문제점이 하나 발생한다. 역전파(backpropagation)시에 각각의 단계의 미분값을 곱해가면서 Input 레이어에 갱신된 가중치 값을 전달하게 되는데, 만약 내부 hidden layer들의 활성화 함수가 모두 sigmoid라면 전달되는 계산값들은 전부 0~1사이다. 왜냐하면 각 단계마다 곱해지는 sigmoid의 미분 값들이 0~0.25사이이기 때문이다.
한편 계단 함수와는 다르게 전 구간이 미분 가능하므로 gradient 값은 0 말고도 0~0.25사이로 다양하다. 즉, gradient를 이용한 '학습'이 가능하다는 것이 계단 함수와는 다른 점이고, 이는 다층 퍼셉트론에서 활성화 함수로 sigmoid가 쓰인 이유이기도 하다.

따라서 sigmoid 함수는 0과 1사이의 값만 다루므로 결국 chain rule을 이용해 계속 그 값을 곱해나간다고 했을 때 결과 값이 0에 수렴해 원래 보존하고자 했던 gradient를 추적할 수 없는, Gradient Vanishing 문제가 생긴다. 또한 지수함수 계산으로 계산이 복잡하고, 함숫값의 중간이 0이 아닌 0.5라서 계산이 더 들어가고 결국 학습시간이 느려진다.
* tanh 함수

sigmoid 함수를 재활용하기 위한 함수. sigmoid 함수의 중간값이 0.5라서 생기는 단점을 극복하기 위해 함숫값 범위를 0~1이 아니라 -1~1로 잡음. 그러나 그래프의 모양이 sigmoid 함수와 같다. 즉, sigmoid 함수와 마찬가지로 tanh 함수도 특정 범위 내에서의 값들만 어느 정도의 gradient를 갖고, 나머지 범위에서는 gradient가 0이라서, 모델의 훈련이 느려지거나 아예 안되는 Gradient Vanishing 문제를 갖고 있다.
* ReLU 함수 (Rectified Linear Unit)

입력값 x가 양수면 그대로 x를 뱉고, x가 음수면 그냥 0을 뱉는 활성화 함수. 기울기가 0에서 1사이 값이 아닌 '1'이기 때문에 Gradient Vanishing 문제를 해결하였다. 또한 함수가 간단해서 계산속도가 빨라 효율적이다. ReLU 등장 이후로 딥러닝이 크게 발전했다. 그러나 중심값이 0이 아니고, x가 음수면 그 결과로 전부 0을 출력하기 때문에 몇몇 가중치들이 갱신되지 않는 문제가 발생한다. (Dying ReLU 문제)
# 요즘엔 sigmoid 보다 ReLU를 더 많이 쓰는데 그 이유는?
Gradient Vanishing 문제가 일어나지 않기 때문
# ReLU의 문제점은?
Dying ReLU 문제. ReLU의 입력값들이 음수면 그 결과로 전부 0을 출력하기 때문에 가중치들이 갱신되지 않는 문제. 이는 활성화 함수 (여기선 ReLU) 의 입력값을 0 근처의 분포로 강제하는 BN으로 해결할 수 있다. (BN 게시물 참고) 즉, 음수 위주의 입력값들을 0 근처로 오도록 분포를 강제하면 입력값이 음수인 현상이 해결된다.
# ReLU로 어떻게 곡선 함수를 근사하나?
ReLU는 선형 부분(y=x 부분)과 비선형 부분(y=0)이 결합된 모양이다. ReLU가 반복 적용되면서 선형 부분의 결합이 이루어지고, 곡선 함수를 근사할 수 있게 된다.
* Leaky ReLU, Parametric ReLU 함수
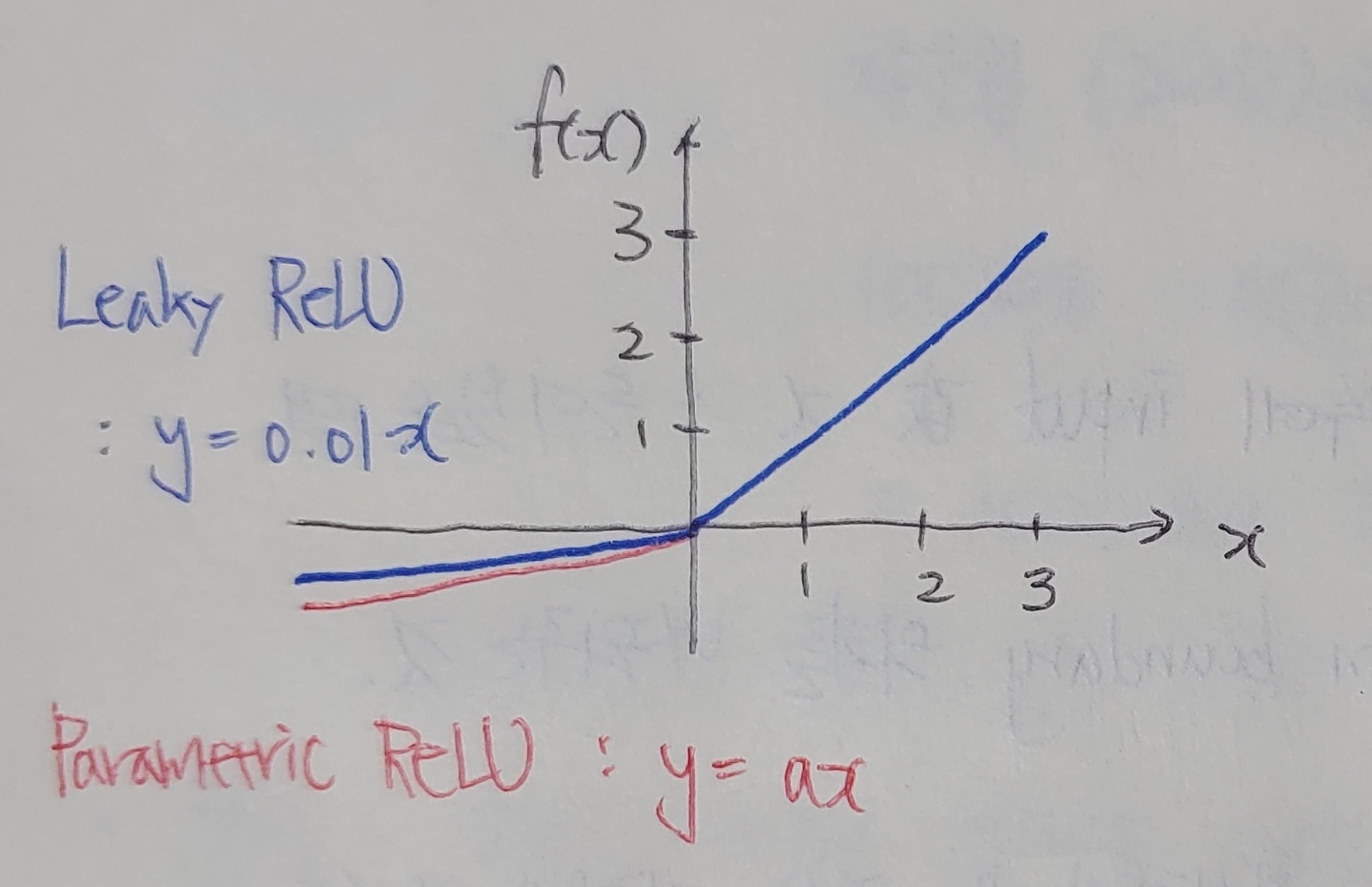
기존의 ReLU 함수에서 x가 음의 값일때 0이 아닌 0.01이나 a의 기울기를 가지도록 하는 함수, 그로써 Dying ReLU 문제를 어느 정도 해결함.