# L1, L2 Norm
Norm은 벡터의 크기를 측정하는 방법이고, 두 벡터 사이의 거리를 측정하는 방법이기도 합니다. L1 Norm은 서로 다른 두 벡터를 나타내는 각 원소들의 차이의 절댓값의 합입니다. L2 Norm은 서로 다른 두 벡터 사이의 유클리드 거리(직선 거리)입니다.
# L1, L2 loss
L1 loss는 실제값과 예측값 사이의 오차의 절댓값 합입니다. 그리고 L2 loss는 실제값과 예측값 사이의 오차 제곱 합입니다. L2 loss는 오차의 제곱 합을 더해나가기 때문에 Outlier(이상치)에 더욱 민감하게 반응합니다. 따라서 L1 loss가 L2 loss에 비해 Outlier에 좀 더 robust, 즉 둔감하다고 할 수 있습니다. 그렇기에 Outlier가 중요한 상황이라면 L1 loss보다 L2 loss를 쓰는 것이 더 좋겠습니다.
# 규제
규제(Regularization)는 자연계에 존재하는 데이터들의 입력과 출력은 서로 매끄럽다는 가정 하에 사용되는 기법입니다. 티호노프는 1960년에 "입력과 출력 사이의 매핑은 매끄럽다."라는 성질을 이용하여 규제 기법을 개발했습니다.
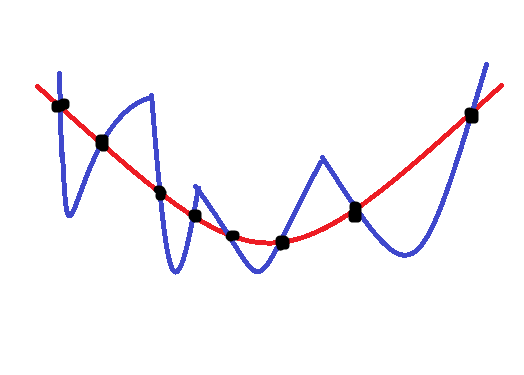
매끄러운 함수와 매끄럽지 않은 함수의 예시는 위와 같습니다. 주어진 까만색 데이터 포인터들을 설명하는 두 모델이지만, 빨간색은 매끄러운(smooth) 함수, 파란색은 매끄럽지 않은 함수를 나타냅니다. 규제 기법은 이처럼 세상의 데이터 대부분은 빨간색 함수처럼 매끄러운 성질을 만족한다는 매우 일반적인 사전 지식을 사용합니다. 따라서 규제의 목적은 매끄럽지 않은 데이터 설명 함수를 매끄럽게 만드는 것입니다.
L1, L2 규제 모두 모델의 오버피팅을 막는 방법입니다. 어떤 데이터에 대해 모델이 훈련 데이터에 대해서만 집중적으로 학습을 많이 해서 w1x1 + w2x2 + ... + w50x50 이라는 다중 선형 회귀 모델을 만들었다고 합시다. 이 모델은 훈련 데이터에 대해서는 예측을 잘 할지 몰라도 나중에 테스트 데이터를 넣었을 때 예측을 잘 못 할 확률이 높습니다. 즉 일반화가 잘 안 되어있다는 뜻입니다.
# L2 규제

L2 규제의 식은 위와 같습니다. 원래의 L2 loss 식에 규제 항이 더해진 모습인데요. 해당 Cost 함수를 가중치 w_i로 미분하게 되면 뒤의 규제 항의 w_i^2들은 모두 w_i로 미분되어 결국 (lambda/2)*w_i라는 일차항들이 남게 됩니다. 따라서 각 w_i들에 대해 비례하게 값이 빠지게 되어, 다중 선형 회귀 모델 식의 w_i들은 완전히 0이 되지 않습니다. 즉 L2 규제를 쓰면 모델의 항을 완전히 없애지는 않습니다.
결론적으로, L2 규제는 크기가 큰 가중치에 대한 규제는 강하게, 작은 가중치에 대한 규제는 약하게 줘서, 모든 가중치들이 모델에게 고르게 반영되도록 합니다. L1 규제에 비해 0으로 수렴하는 가중치들은 적습니다.
이러한 L2 규제의 성질 때문에, L2 규제를 가중치 감쇠 기법이라고도 부릅니다.
수식을 좀 더 자세히 뜯어보면 아래 필기와 같습니다.

# L1 규제

L1 규제의 식은 위와 같습니다. 원래의 L1 loss 식에 규제 항이 더해진 모습인데요. 이 Cost 함수를 가중치 w_i로 미분하게 되면 결론적으로 뒤의 규제 항의 w_i들은 모두 1까지 미분되어 결국 (lambda/2)라는 상수항만 남게 됩니다. 이때 가중치 업데이트는 원래 가중치에서 Cost 함수를 가중치 w_i로 미분한 값과 학습률을 곱한 값이 빠지면서 이루어집니다.
고정된 상수값 (lambda/2)가 모든 항에 대해 공평하게 빠지면서 자잘한 가중치 다중 선형 회귀 모델 식에서의 w_i들은 0으로 가버리고 중요한 가중치만 남아서 feature 수가 줄어드므로 과적합을 막게 됩니다. 즉 L1 규제를 쓰면 모델의 항 몇 개를 완전히 없애게 됩니다. 따라서 모델을 sparse하게 만든다고 보면 됩니다.
결론적으로, L1규제는 크기가 작은 가중치들을 거의 0으로 수렴시켜 모델에게 중요한 가중치만 남도록 만듭니다. 즉, L1 규제가 L2 규제보다 더욱 간헐적으로(sparsely) 가중치를 가지기 때문에 L1 규제보다 오버피팅 방지에 효과적입니다. 아래를 참고하세요.

수식을 좀 더 자세히 뜯어보면 아래 필기와 같습니다.

# L1, L2 규제 그림 설명

위는 L1과 L2 규제를 그림으로 설명한 것입니다. 두 개의 가중치만을 생각했을 때, L1 Norm을 만족하는 가중치 영역의 그래프가 있고, L2 Norm을 만족하는 가중치 영역의 그래프가 있다고 가정합시다. 그럼 L1의 경우 마름모, L2의 경우 원형의 그래프를 가질 텐데요.
그리고 안쪽으로 갈수록 점점 그 값이 0에 가까워지는, 두 가중치에 따른 손실(Loss)함수의 landscape가 있다고 합시다. 가중치 후보는 무수히 많지만, 해당 Loss landscape는 L1 규제일 때 마름모의 꼭짓점, L2 규제일 때 원의 접점에서 가장 최솟값(최적값)을 가지게 됩니다.
이때, 보시는 것과 같이 L1 규제를 사용하는 경우, 최적 가중치 값을 가질 때의 Loss landscape가 가중치 영역 그래프의 꼭짓점에 위치할 확률, 즉 두 가중치 중 하나가 0일 확률이 L2 규제를 사용하는 경우보다 높습니다. 따라서 L1 규제일 때 더 기하학적으로 뾰족한 모양을 갖고 있기 때문에 최적 해가 어느 축에서 결정될 확률이 높다고 말할 수도 있습니다.
이로써 왜 L1 규제를 사용할 때 0인 가중치가 더 많이 생기는지를 업데이트 수식뿐만 아니라 그림으로도 알 수 있었습니다.
더 좋은 이야기들 및 출처:
'딥러닝 & 머신러닝 > 머신러닝 지식' 카테고리의 다른 글
| 바이어스와 분산 트레이드 오프 (bias and variance trade-off) (0) | 2020.12.08 |
|---|---|
| 선형 함수 (linear function) (0) | 2020.11.12 |
| 교차 검증 (Cross Validation) & 훈련/검증/테스트 데이터 (0) | 2020.08.05 |
| 차원의 저주와 차원 축소 개념 (0) | 2020.08.05 |
| 정규화(Normalization)의 목적과 방법들 (0) | 2020.08.04 |


