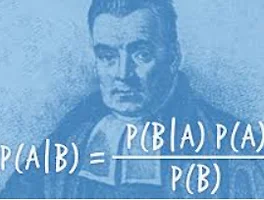 나이브 베이즈 분류기 (Naive Bayes Classifier)
이번 글에서는 나이브 베이즈 분류기(Naive Bayes Classifier)에 대한 이론적 지식을 알아보겠습니다. 베이즈 정리, 최대 우도 추정, 최대 사후확률 추정, 둘 간의 비교, '나이브'의 뜻, 라플라스 스무딩, 나이브 베이즈 분류기의 특징 순서로 정리하겠습니다. 1. 베이즈 정리 베이즈 정리(Bayes Theorm)는 이름에서도 알 수 있듯이, 나이브 베이즈 분류기의 근본이 되는 수학 정리입니다. 베이즈 정리는 두 사건 X, Y에 대한 조건부 확률(conditional probability) 간에 성립하는 확률 관계이며, 수식은 다음과 같습니다. 수식 중 P(X|Y), P(Y|X)라는 것이 바로 조건부 확률을 나타내는 표현입니다. 예를 들어 P(A|B)라는 확률은 사건 B가 일어났다는 가정 하..
나이브 베이즈 분류기 (Naive Bayes Classifier)
이번 글에서는 나이브 베이즈 분류기(Naive Bayes Classifier)에 대한 이론적 지식을 알아보겠습니다. 베이즈 정리, 최대 우도 추정, 최대 사후확률 추정, 둘 간의 비교, '나이브'의 뜻, 라플라스 스무딩, 나이브 베이즈 분류기의 특징 순서로 정리하겠습니다. 1. 베이즈 정리 베이즈 정리(Bayes Theorm)는 이름에서도 알 수 있듯이, 나이브 베이즈 분류기의 근본이 되는 수학 정리입니다. 베이즈 정리는 두 사건 X, Y에 대한 조건부 확률(conditional probability) 간에 성립하는 확률 관계이며, 수식은 다음과 같습니다. 수식 중 P(X|Y), P(Y|X)라는 것이 바로 조건부 확률을 나타내는 표현입니다. 예를 들어 P(A|B)라는 확률은 사건 B가 일어났다는 가정 하..