이번 포스팅에선 Novel-view synthesis task에서 획기적 방법을 제시한 3D Gaussian Splatting (3DGS) 에 대해 리뷰하겠습니다.
3D Scene Reconstruction

3D Scene Reconstruction은 여러 각도에서 촬영한 2D 이미지를 기반으로 장면의 3D 구조를 재구성하는 기술입니다.
이를 통해 장면의 깊이, 기하학적 관계, 표면 구조 등을 포함한 3D 모델을 생성하여 컴퓨터가 더 잘 이해하고 처리할 수 있도록 합니다. 이러한 기술은 3D 모델링, SLAM, AR & VR, 자율주행과 같은 다양한 분야에서 중요한 역할을 합니다.
3D Scene Reconstruction은 딥러닝 등장 이전부터 연구되어 온 분야입니다. 초기에는 컴퓨터 비전 알고리즘을 활용한 전통적인 기법들이 주를 이루었으며, 대표적으로 Structure-from-Motion (SfM)이나 Multi-View Stereo (MVS) 같은 방법론이 있습니다.
이들은 여러 이미지를 사용해 카메라의 위치와 장면의 3D 구조를 계산하는 방식을 기반으로 했습니다. 3D Scene Reconstruction을 하기 위한 기본 단위로 Meshes와 points를 채택했는데요. 이들은 가장 일반적인 3D scene 표현 방식으로, 명시적(explicit)이고 GPU/CUDA 기반 rasterization에 적합하기 때문입니다.
(Mesh: 표면 또는 솔리드 형상을 나타내는 사각형과 삼각형의 모음 / rasterization : 3D를 2D로 표현하는 방법)
그럼에도 불구하고, 이들은 새로운 시점 합성 (Novel-view synthesis) 에서 어려움을 겪었습니다.
Structure-from-Motion (SfM)
본격적인 Novel-view synthesis 설명 전에, 위에서 언급한 Structure-from-Motion, SfM에 대해서 알아보겠습니다.
SfM은 동일 객체를 다른 시점에서 찍은 multi-view 이미지로부터, 3D 구조와 카메라 포즈를 reconstruction 하는 프로세스입니다. 대표적 방법으로는 COLMAP이 있습니다.

COLMAP을 통해 생성된 point들 하나하나가 모여서 콜로세움과 그 주변의 풍경을 reconstruction한 모습입니다. 빨간색 점들 하나하나가 카메라를 뜻하며, 실제 COLMAP 소프트웨어에서 카메라를 눌러보면 그 카메라의 정보가 나옵니다. 이 수많은 카메라들이 촬영한 방향의 사진을 활용해서, 보시는 바와 같이 3D 구조가 reconstruction 된 것입니다.
SfM을 통해, 3DGS의 입력으로 사용되는 Camera parameter를 얻을 수 있습니다.
Camera parameter는 월드 좌표계의 3D 복셀 좌표를 카메라 좌표계를 거쳐, 픽셀 좌표계의 2D 픽셀 좌표로 변환하는 파라미터입니다. Extrinsic parameter [R|t] 와 Intrinsic parameter K 의 행렬곱 P 로 이루어집니다.
Extrinsic parameter (= Camera pose) 는 3D 공간에서 카메라가 어디에 위치하고 (3D Translation) 어디를 바라보는지를 (3D Rotation) 나타냅니다. 월드 좌표계 → 카메라 좌표계로 변환시켜주는 파라미터이기도 합니다.
Intrinsic parameter는 초점 거리 (fx, fy), 주점 (cx, cy), 비대칭 계수 (skew) 등 카메라 렌즈와 센서 위치에 의해 결정되는 파라미터입니다. 이미지 패널이 얼마나 이동하고 (2D Translation), 얼마나 확대되고 (2D Scaling), 얼마나 기울어졌는지 (2D Shear) 나타냅니다. 카메라 좌표계 → 이미지 좌표계 로 변환시켜주는 파라미터이기도 합니다.
NeRF (Neural Radiance Fields)

우선, Radiance Field는 3D 공간에서 빛의 분포를 나타내는 표현으로, 장면의 색상과 밀도를 수학적으로 정의합니다. 이는 추상적인 3D 표현이기 때문에 인간이 직접적으로 이해하거나 시각화하기 어렵습니다. 이를 해결하기 위해 Radiance Field를 특정 카메라 시점에서 2D 이미지로 렌더링하는 다음 과정을 거칩니다:
- 특정 카메라 뷰로부터 픽셀 위치와 광선 (ray) 방향을 샘플링합니다.
- 샘플링된 광선 방향을 따라 일정 간격으로 3D 위치를 추출합니다.
- 추출된 위치들을 Radiance Field에 입력하여 해당 지점의 색상과 밀도를 계산합니다.
- 계산된 색상과 밀도를 기반으로, 각 광선에서의 Volume Rendering을 통해 픽셀의 최종 색상을 결정합니다.
즉, Radiance Field는 3D 장면의 근본적 표현이고, 2D 렌더링은 이를 활용해 관찰 가능한 이미지를 생성하는 과정입니다.
렌더링을 좀 더 풀어서 설명하자면, 3D 공간의 장면을 2D 이미지로 변환하는 과정이라고 할 수 있습니다. 렌더링을 거쳐서 화면 속에 나타난 2D 이미지는 마치 3D 공간에 있는 것처럼 보입니다.
따라서 Neural Radiance Fields, NeRF는 3D 공간에서 빛의 분포, 즉 3D 장면을 신경망 (MLP) 기반의 Radiance Field로 표현하고, 이를 바탕으로 다양한 시점 (novel views) 의 2D 이미지로 렌더링하기 위해 고안된 컴퓨터 비전 기술이라고 할 수 있습니다.
NeRF는 특정 장면의 모든 시점을 학습하고, 관찰되지 않은 시점에서도 사실적인 이미지를 합성하는 Novel View Synthesis에 특화되어 있습니다. 이 기술은 전통적인 3D 객체 생성 방식이 아닌, 3D 장면을 관찰하는 모든 시점의 뷰(View)를 생성하는 새로운 접근법을 제안하며, 장면의 표현과 렌더링 방식을 근본적으로 재정의했습니다.
NeRF는 3D 공간의 장면을 연속적인 표현으로 학습하는 신경망 (MLP) 기반의 Radiance Field로, 다음과 같은 입력과 출력을 통해 함수처럼 작동합니다:
- 입력 (Input): 포인트의 위치 (x, y, z) , 해당 위치에서 광선의 방향 (θ, ϕ)
- 출력 (Output): 해당 광선에서의 RGB 색상 값 (R, G, B) , 해당 위치에서의 밀도 값 (σ)
따라서, NeRF란 특정 포인트의 위치 & 방향 값을 Input으로 주면 Output으로 RGB & 밀도 값을 주는 신경망 기반의 함수라고도 볼 수 있습니다.
NeRF는 기본적으로 공간과 광선 정보를 조합하여, 광선이 장면을 통과하면서 상호작용하는 방법을 모델링합니다. Radiance Field 설명에서도 잠깐 언급되었듯, 이를 위해 다음과 같은 기법을 사용합니다:
- Volume Rendering: 장면의 특정 방향에서 볼 수 있는 색상 값을 적분 계산하여 최종 이미지를 합성.
- MLP (Multi-Layer Perceptron): 신경망이 공간의 밀도와 색상을 학습하도록 설계
NeRF는 3D Scene Reconstruction과 Novel View Synthesis를 위한 강력한 방법이지만, 훈련 및 렌더링에 긴 시간이 필요하다는 한계가 있습니다. 수백 개의 이미지로부터 장면의 밀도와 색상을 추정하는 데 대규모 계산이 필요하며, 특히 고화질 결과물을 도출할수록 MLP 기반 모델의 계산 복잡도가 크게 증가하기 때문입니다.
3DGS 논문에 따르면, 최근의 NeRF 기법들은 continuous representation을 기반으로 동작하며, 이는 voxel, hash grids, 또는 points에 저장된 값을 interpolation하여 활용한다고 합니다. 하지만 이러한 방법들의 continuous 특성은 장면 표현의 최적화에 유리하지만, 렌더링에 필요한 3D 포인트들을 매번 stochastic sampling 해야 하기 때문에 많은 연산량과 noise를 초래합니다.
3DGS (3D Gaussian Splatting)
NeRF와의 차이점

3DGS는 기존의 NeRF와는 꽤나 다른 방식을 사용하여 3D 장면을 synthesis하는 기술입니다. NeRF가 포인트의 위치와 해당 위치에서 광선의 방향을 입력값으로 받는 MLP를 활용하여 장면의 색상과 밀도를 추정해야 하는 반면, 3DGS는 3D Gaussian들의 조합을 이용해서 3D 장면의 색상과 밀도를 예측합니다.
이 3D Gaussian들은 3D 장면의 구조와 속성을 이산적으로 표현하며, 이미 색상과 밀도 정보를 포함하고 있습니다. 이러한 특징 덕분에 3DGS는 NeRF처럼 각 지점에서 MLP에게 정보를 요청 (query) 하는 과정 없이, 새로운 시점에서의 장면을 즉각적으로 빠르게 생성할 수 있습니다.
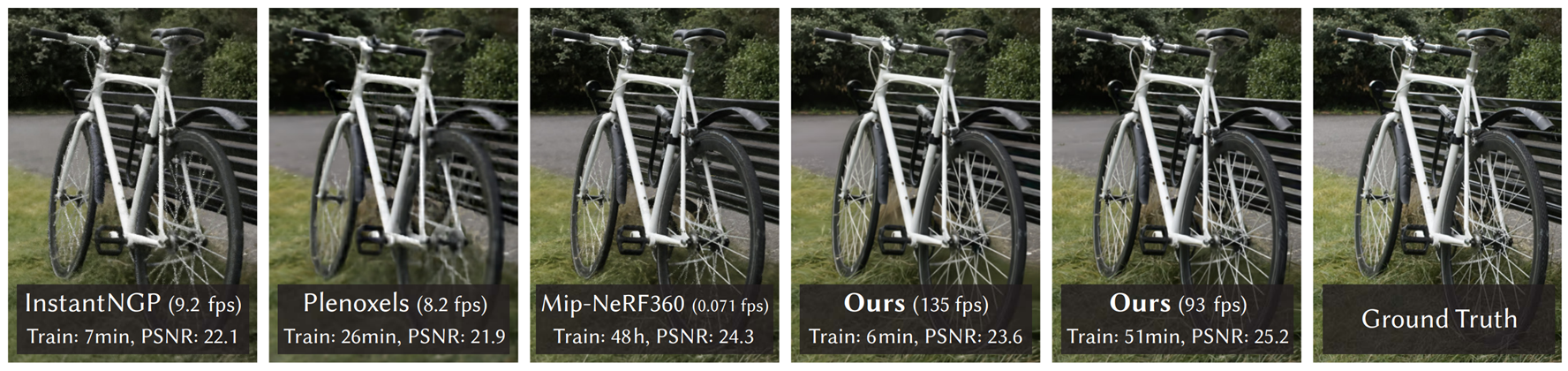
이 방식은 렌더링 속도와 학습 시간에서 NeRF를 압도적으로 능가합니다. 3DGS는 3D Gaussian 기반의 표현 덕분에 새로운 시점의 장면을 실시간에 가까운 속도로 렌더링할 수 있으며, 훈련 역시 몇 분 안에 완료될 정도로 효율적입니다. 시각적 성능에서도 3DGS는 기존 NeRF와 동등하거나 더 나은 품질을 제공하며, 특히 PSNR 측면에서 뛰어난 결과를 보입니다.
Implicit & Explicit Radiance Field
NeRF와 3DGS의 특성을 이해하는데 implict & explicit radiance field의 개념이 있으면 좋습니다.
먼저 Radiance field는 3D 공간에서 빛의 분포를 나타내는 표현이라고 위에서 설명했습니다.
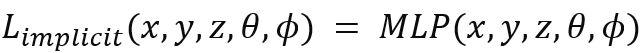
이때 Implicit Radiance Field란 블랙박스처럼 빛 분포를 표현하는 방식입니다. 마치 NeRF의 MLP처럼, 구조가 감춰져있는 암묵적인 표현법이라고 할 수 있습니다. 단점은 계산량이 많다는 것입니다.
위 표현법을 사용해 NeRF를 다시 설명해보겠습니다. NeRF는 implicit neural scene representation을 학습하는 모델로, 포인트의 3D 좌표 (x, y, z)와 광선의 방향 (θ, ϕ)를 색상과 밀도로 매핑하는 volume rendering function을 기반으로 동작합니다. NeRF를 통해 표현된 빛 분포는 implicit radiance field입니다.
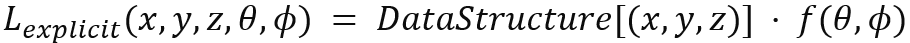
그리고 Explicit Radiance Field란 이산적인 공간 데이터로 빛 분포를 표현하는 방식입니다. 마치 voxel grid, a set of points처럼, 명시적이고 구조화된 데이터 기반으로 장면을 표현합니다. 단점은 메모리 사용량이 많다는 것입니다.
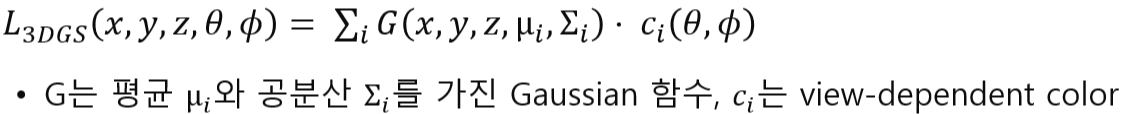
3DGS는 둘의 장점을 합친 하이브리드형 Radiance Field 표현 방법입니다. 뒤에서 좀 더 자세히 설명하겠지만, 요약하자면 3DGS는 다양한 시점에서 촬영한 multi-view 이미지로부터 얻은 3D Gaussian들의 위치, 공분산, 투명도, 색상 파라미터를, gradient descent 방식으로 최적화해가며 3D 장면을 표현하는 기법입니다.
즉, 3DGS는 신경망 (implicit) 기반 최적화의 이점과, 유연하지만 (= 최적화에 따라 바뀔 수 있지만) 명시적이고 구조화된 데이터 (explicit) 활용의 장점을 결합한 Radiance Field라고 할 수 있습니다.
What is “3D Gaussian” and “Splatting”?
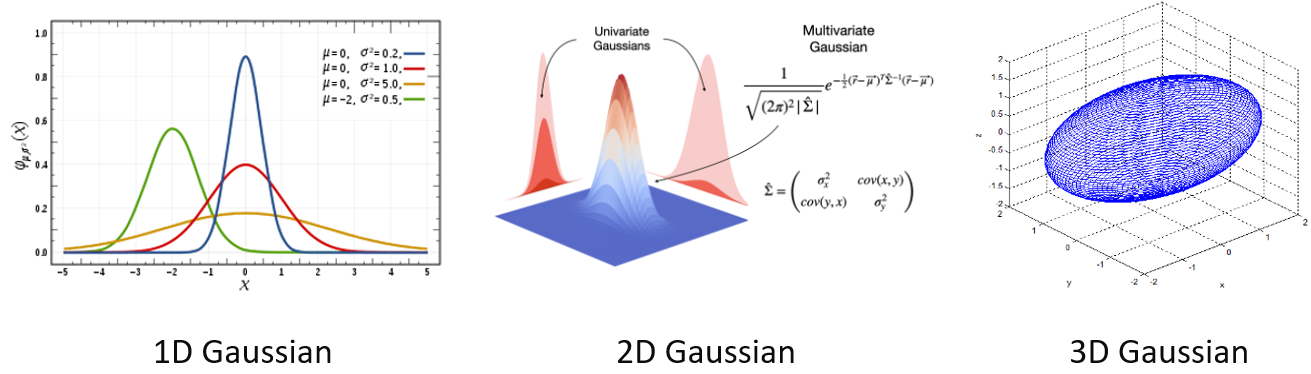
3D Gaussian이란 3차원 공간에서의 가우시안 (정규) 분포를 뜻합니다. 1차원의 가우시안 분포는 우리가 흔히 아는 형태이며, 2D 가우시안 분포는 1차원 가우시안 분포 두개를 통해 결정됩니다. 3D 가우시안 분포도 비슷하게 생각될 수 있습니다.
한편 지금까지 설명한 3D Gaussian을 정확히는 anisotropic 3D Gaussian이라고 표현해야 하지만, 편의상 이후에도 3D Gaussian으로 명명하겠습니다. anisotropic, 한국말로 비등방성이란, 특정 속성이 방향에 따라 변하는 성질을 뜻합니다. 위 그림처럼 3DGS에서의 3D Gaussian은 방향에 따라 다른 반지름을 갖고 있기 때문에, 우리가 보는 방향에 따라 그 모양이 다르게 보입니다. 따라서 3DGS에서의 3D Gaussian은 anisotropic 합니다.
나중에 더 설명하겠지만, 이 3D Gaussian은 결국 빛의 분포를 설명하는 수학 모델인 Radiance Field를 형성할 때 쓰이기 때문에, 3D Gaussian을 보는 방향에 따라 그 모양 뿐만 아니라 색상, 투명도 등도 달라지는 뷰 의존적 (view-dependent) 특성을 가져야 합니다. 이는 3D Gaussian이 anisotropic 해야하는 결정적 이유이기도 합니다.
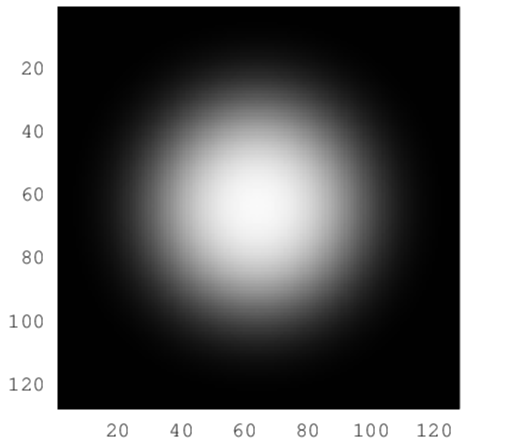
3D Gaussian은 특정 위치를 중심으로 할 때, 가장자리로 갈수록 그 값이 감소하는 특징을 가집니다. 쉽게 말해, 위의 Gaussian Blur 필터처럼 끝으로 갈수록 뿌연 점구름을 뜻합니다. 3D Gaussian은 평균 (mean) 과 공분산 (covariance) 으로 그 위치와 크기 및 방향이 결정됩니다. 참고로, 위 3D Gaussian은 어느 방향에서 봐도 그 모양이 같기 때문에 isotropic (등방성) 하다고 할 수 있습니다.

Splatting이란 물기를 머금은 뭔가가 부딪치는 모습에 대한 의성어를 뜻합니다.

따라서 3D Gaussian Splatting이란, 3D 공간 상에 수많은 3D Gaussian을 흩뿌린 후 겹쳐지게 조정해, 하나의 장면을 구성하는 것이라고 생각할 수 있습니다. 비유하자면, 공간상에 M&M’s 초콜릿들을 흩뿌린 다음에, 주어진 사진과 똑같아질 때까지 초콜릿들의 위치, 크기 및 방향, 추가적으로 색깔과 투명도를 바꿔주는 방법과 비슷합니다. 이때 초콜릿은 서로 겹쳐도 됩니다.

위 그림은 Mip-Splatting Demo 중 "Garden"에서 가져온 이미지입니다. 정원의 3D 장면을 렌더링 하기 위해, 녹색의 뾰족뾰족한 3D Gaussian들이 수없이 겹쳐진 모습을 확인할 수 있습니다. [Mip-Splatting Demo]
3DGS Process: Why 3D Gaussian?
그럼 왜 Novel-view synthesis를 위해, 다시 말해, 왜 3D 장면을 Radiance field로 표현하기 위해 3D Gaussian을 기본 단위 (primitive) 로 삼았을까요?
우선, 3D 장면의 geometry를 모델링해야 3D 장면을 Radiance field로 표현할 수 있다는 사실을 알아야 합니다. 중요한 개념이라 다시 설명 드립니다. Radiance Field는 3D 공간에서 빛의 분포를 나타내는 표현으로, 입력되는 위치와 방향에 따라 빛의 색상과 밀도 (= 투명도) 를 도출하는 함수입니다.
즉, 3D 장면의 geometry인 특정 위치와 방향을 알고 있어야 3D 장면을 알맞은 색상과 밀도로 표현할 수 있게 됩니다.
3DGS는 기존의 NeRF와 유사하게, SfM으로 보정된 camera parameter 값을 입력으로 사용하며, SfM에서 생성된 포인트들을 기반으로 3DGS 과정이 진행됩니다. 따라서 3DGS 과정은 이전의 2D 포인트 기반 방법과 유사합니다. 해당 방법들은 각 포인트를 작은 평면상의 원으로 가정하며, 그로부터 추정한 normal vector를 기반으로 3D 장면의 geometry를 모델링합니다.
하지만 SfM 포인트의 희소성 (sparsity) 때문에 normal vector를 추정하는 것은 매우 어렵고, 추정된 noisy한 normal vector를 최적화하는 것도 힘듭니다. 이러한 문제들 때문에, 3DGS에선 normal vector가 필요없는, 3D Gaussian으로 3D 장면의 geometry를 모델링합니다.
즉, 3DGS의 목표는 sparse한 (SfM으로 얻어진) 포인트 집합에서 시작해, normal vector 없이도 고품질 novel-view synthesis를 가능하게 하는 3D 장면 표현을 최적화하는 것입니다.
이를 위해, 미분 가능한 부피 표현 (differentiable volumetric representation) 특성을 가짐과 동시에, 비구조적 (unstructured) 이고 명시적 (explicit) 표현 방식을 사용해 매우 빠른 렌더링이 가능해야 합니다.
이를 만족하는 기본 단위가 바로 3D Gaussians이며, 이는 미분 가능하고 2D Gaussian (splats) 으로 쉽게 projection 할 수 있어, 렌더링 시 빠른 α-blending (projection 된 2D Gaussian의 혼합을 통해 특정 장면의 색상 및 투명도를 표현하는 기술) 을 가능하게 합니다.
또한 미분이 가능하기에 3D 장면을 표현하는 3D Gaussian이 학습 가능해지고 (learnable), 학습이 가능하기 때문에 최적의 3D 장면을 표현하는 최적의 3D Gaussian들을 찾을 수 있게 됩니다.
(2D projection과 α-blending은 Rasterization 과정에 속합니다. 이 과정들은 뒤에서 자세히 설명합니다)
(3D Gaussian을 2D 이미지 공간에 projection 하면 2D Gaussian이 되고, 2D Gaussian = 2D splats 입니다)
요약해보면, 3D 장면을 Radiance Field로써 표현하기 위해 3D Gaussians을 기본 단위로 삼은 이유는 다음과 같습니다:
- Normal Vector 불필요
- 기존 방법은 SfM 포인트의 희소성 때문에 normal vector를 추정하는데 어려움이 있음.
- 게다가 noisy한 normal vector을 최적화하는 것도 힘듦.
- 3D Gaussian은 normal vector 없이도 3D 장면의 geometry를 모델링할 수 있음.
- Differentiable Volumetric Representation
- 3D Gaussian은 미분 가능한 부피 표현으로, Radiance Field의 최적화를 효과적으로 수행할 수 있음.
- 즉, 미분을 통해 나오는 gradient를 이용해, 3D Gaussian을 구성하는 파라미터를 학습할 수 있음.
- Unstructured & Explicit Representation
- 비구조적 & 명시적 표현 방식으로, 유연성과 빠른 연산을 모두 제공. 이는 매우 빠른 렌더링으로 이어짐.
- 효율적인 2D Projection과 α-Blending
- 3D Gaussian은 2D Gaussian으로 쉽게 projection 되며, 빠른 α-blending을 통해 실시간 렌더링 가능함.
NeRF 파트의 Radiance Field 정의를 가져와 다시 요약해보자면, 3DGS의 목적은 3D 장면을 3D Gaussian 기반의 Radiance Field로 표현하여, 다양한 시점에서 2D 이미지를 렌더링할 수 있도록 하는 것입니다. (3DGS가 궁극적으로 3D 장면을 표현하는 것인지, 2D 장면을 표현하는 것인지 헷갈려서 목적을 다시 한번 명확히 해보았습니다)
Overview of 3DGS Process

3DGS가 동작하는 큰 그림을 간단히 설명해보겠습니다.
3DGS Process: Initialization

1. Mean (M, µ) : 3D Gaussian의 평균으로써, 3D Gaussian의 위치 결정
기존의 NeRF와 유사하게, SfM으로 보정된 camera parameter 값을 입력으로 사용하며, SfM에서 생성된 포인트들을 기반으로 sparse point cloud를 만들어 초기 3D Gaussian으로 활용합니다. 그렇다면 그 포인트로부터 어떤 정보를 사용하는걸까요?
3D Gaussian은 SfM으로 생성된 포인트들의 '좌표'를 그것의 Mean (µ), 즉 평균으로 설정합니다. 그리고 이는 곧 3D Gaussian의 중심, 즉, 위치를 결정했다는 말과 동일합니다. 이 '위치'는 위 알고리즘의 'M' 그리고 'µ' 에 해당합니다.
3DGS는 포인트 하나하나로부터 좌표를 구해서 그것을 3D Gaussian의 위치로 삼으므로, 포인트 개수만큼 3D Gaussian이 생성됩니다. 즉, 높은 Novel-view synthesis 성능을 위해선 SfM을 통해 최대한 많은 포인트들을 장면들로부터 얻어와야 한다는 사실도 알 수 있습니다. 그러기 위해선 포인트들을 잘 추출하는 SfM을 사용하거나, SfM이 잘 동작하게끔 장면들을 캡쳐해야 하겠습니다.
2. Covariance (S, σ) : 3D Gaussian의 공분산으로써, 3D Gaussian의 크기, 방향 결정
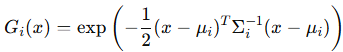
픽셀 x에 대해서, 평균 µ를 중심으로 하는 i번째 3D Gaussian은 위와 같이 Σ를 통해 표현됩니다. Σ는 월드 좌표계에서 정의된 3x3의 3D covariance matrix로, 3D Gaussian의 크기와 방향을 정의하는데 사용됩니다. Covarinace, 즉, 이 '공분산'은 위 알고리즘의 'S' 그리고 'σ'에 해당합니다.
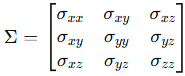
이 3D covariance matrix의 각 요소는 3D Gaussian의 공간 내 분포와 상관성을 나타냅니다. 구체적으로, Σ의 내부 값들은 다음을 의미합니다:
- 대각선 요소 (σ_xx, σ_yy, σ_zz)
- 각각 x, , z 축 방향으로의 분산 (variance) 을 나타냅니다.
- 분산은 해당 방향으로 Gaussian이 얼마나 넓게 퍼져 있는지를 나타내며, 값이 클수록 분포가 더 넓게 퍼져 있음을 의미합니다.
- 비대각선 요소 (σ_xy,σ_xz,σ_yz)
- 와 , x와 , y와 z 축 간의 공분산 (covariance) 을 나타냅니다.
- 공분산은 두 축 간의 상관관계를 표현하며, 값이 양수이면 두 방향이 양의 상관관계 (같은 방향으로 변화), 음수이면 음의 상관관계 (반대 방향으로 변화) 를 가집니다.
- 값이 0이라면 해당 축 간에 독립적인 관계임을 의미합니다.
그럼 이제 Σ를 최적화하여 딱 알맞는 Σ를 얻고, 그 Σ를 이용해 3D Gaussian을 정의 후 Novel-view synthesis 하면 되겠습니다. 이때, Σ는 3x3의 3D covariance matrix라고 했습니다. 그럼 Σ의 각각 요소를 gradient descent 방식으로 찾아나가서 최적화하면 되지 않을까요?
안됩니다. 왜냐하면 본래 covariance라는 것은 postive semi-definte 해야 물리적으로 의미가 있는데, gradient descent 방식으로 구하는 3D covariance matrix가 postive semi-definte 하지 못 할 가능성이 매우 크기 때문입니다.

postive semi-definte 특성을 위에 작성했습니다. 왜 이게 공분산 행렬에게 중요할까요? 선형 대수학적 안정성을 통한 계산 가능성 보장, 기하학적으로 유효한 형태의 3D Gaussian 보장 등의 이유가 있지만, 좀 더 직관적이고 이해가 쉬운 이유가 있습니다.
x^TAx >= 0 조건을 만족하려면, A의 대각선 요소는 항상 0 또는 양수여야 합니다. 이때 위에서도 말했듯이, 3D 공분산 행렬의 대각선 요소들은 각각 x, , z 축 방향으로의 분산을 뜻하는데, 분산은 표준편차의 '제곱'값이므로 무조건 양수입니다. 따라서 지금 다루는 3D 공분산 행렬 뿐만 아니라 모든 공분산 행렬는 postive semi-definte 해야 합니다.
그런데 gradient descent 방식으로 3D 공분산 행렬 내부 요소를 구한다면, 대각선 요소가 음수가 나올수도 있을 것이고, 그럼 postive semi-definte를 만족하지 못하게 됩니다. 그렇게 되면 물리적으로 의미없는 공분산이 되어버리므로, 3D Gaussian을 초기에 형성할 때도 문제가 되며, 이는 성능 하락 또는 동작 자체가 불가능한 상태로 이어질 것입니다.
이러한 문제를 해결하기 위해 저자들은 이 3x3의 3D 공분산 행렬 표현을 아래처럼 바꿔주는 방식을 택했습니다. 즉, scaling과 rotation을 독립적으로 최적화하여 공분산 행렬이 유효하도록 만들어 준 것입니다.
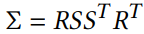
Σ라는 이 3D 공분산 행렬는 Scaling matrix S와 Rotation matrix R을 통해, 위 수식과 같이 정의됩니다. 여기서 S는 각 축 방향의 3D Gaussian의 크기를 조절하고, R은 3D Gaussian의 회전 방향을 결정합니다. 따라서 Σ는 3D Gaussian의 크기 방향을 나타내게 됩니다. S와 R은 scaling과 rotation을 독립적으로 최적화할 수 있도록 각각 3D 벡터 s와 쿼터니언 (quaternion) q를 개별적으로 저장하고 있습니다. (쿼터니언은 rotation 표현 방법 중 하나입니다)
이때 3D 벡터 s는 x,y,z축에 관한 배율 정보를 갖고 있습니다. 그리고 q는 4x1 형태이며, 3x3 형태의 Rotation matrix R로 변환됩니다. (코드의 build_rotation, build_scaling_rotation에서 확인할 수 있습니다) 이처럼 이들은 각 행렬로 쉽게 변환 가능하며, 특히 쿼터니언 q는 정규화 과정을 통해 유효한 단위 쿼터니언으로 유지됩니다.
한편 3D Gaussian을 통해 3D 장면을 Radiance Field로 표현한다고 해도, 이를 2D 평면에서 표현하는 작업인 렌더링이 필요합니다. (렌더링의 정의는 NeRF 파트에서 설명했습니다) 따라서 장면을 표현하고 있는 3D Gaussian들을 2D로 projection 해야 합니다.
Zwicker [2001a] 등은 3D Gaussian들을 2D 이미지 공간으로 projection 하는 방법을 제시했습니다. 3D Gaussian들을 2D로 projection 해서 2D Gaussian으로 만들어주는, 카메라 좌표계에서의 공분산 행렬 Σ′는 아래와 같이 계산됩니다.
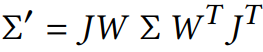
수식의 구성요소는 다음과 같습니다:
- W : Viewing transformation matrix (월드 좌표계 → 카메라 좌표계로 변환해주는 행렬 = 관점 변환 행렬)
- J : Projective transformation matrix (카메라 좌표계 → 월드 좌표계로 변환해주는 행렬 = 투영 변환 행렬) 의 affine 근사에 대한 Jacobian (특정 행렬의 미분).
- Σ : 3D covariance matrix (3D Gaussian의 크기와 방향 결정)
위 수식은 Σ를 월드 좌표계에서 카메라 좌표계로 변환해주고, 다시 카메라 좌표계에서 선형 근사 (≈ affine 근사) 를 통해 Σ를 2D 이미지 평면으로 projection 합니다. 왜 Σ를 월드 좌표계에서 카메라 좌표계로 변환해주는 과정이 필요할까요? 렌더링의 핵심은 카메라가 보는 관점에서 장면을 2D로 표현하는 것이기 때문입니다.
(월드 좌표계와 카메라 좌표계에 관한 설명은 제 블로그의 또 다른 글을 참고하면 좋습니다)
수식에 대해 좀 더 자세히 살펴보겠습니다.
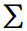
1. 렌더링을 통해 3D 공간의 정보를 2D 평면에 표현하려면, 3D Gaussian을 2D 이미지 평면으로 projection 해야 합니다. 이때, 3D Gaussian의 중심뿐만 아니라, 3D Gaussian 분포의 크기와 방향을 나타내는 위 Σ도 함께 변환되어야 합니다.
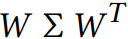
2. 이제, 월드 좌표계에서 카메라 좌표계로의 변환을 위해 관점 변환 행렬 W를 사용합니다. 이 행렬은 3D Gaussian의 위치와 방향을 카메라 관점에서 재정의합니다. 공분산 행렬의 Positive Semi-Definite 특성과 대칭성을 보존하기 위해, 변환 시 W와 그 전치 행렬 W^T를 함께 사용하여, 를 먼저 위 수식과 같이 변환합니다.
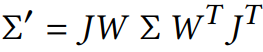
3. 카메라 좌표계에서 2D 이미지 평면으로의 projection은 일반적으로 비선형 변환입니다. 이를 선형 근사하기 위해 Jacobian 행렬 J를 도입합니다. 이때의 Jacobian은 특정 투영 변환 행렬의 미분을 나타내며, 각 축에 대한 변화를 선형적으로 근사합니다. J와 그것의 전치 행렬 J^T를 사용해 공분산 행렬의 변화를 반영하고, 최종적으로 위와 같이 나타냅니다.
한편 Σ'는 3차원의 공분산 값을 계산하므로 3x3 행렬이 됩니다. 그런데 앞서 언급한 Zwicker [2001a] 등은 3D Gaussian을 한쪽 축으로 적분하면 2D Gaussian과 동일한 값을 가지기 때문에, 3번째 행과 열을 버릴 수 있다고 합니다.
따라서 Σ'는 3x3 행렬 대신에 2x2 행렬로 표현할 수 있게 됩니다. 이는 '평면' 상의 점과 법선을 기반으로 계산된 covariance 행렬과 동일한 구조와 속성을 가집니다. 즉, 2D Gaussian 분포를 표현하기에 충분한 정보를 포함합니다.
3. Color (C, c) : 3D Gaussian의 색깔 결정
논문에 따르면 radiance field의 directional appearance (color) 는 spherical harmonics (SH) 에 의해 표현된다고 합니다. 즉, 3DGS 과정으로 도출된 3D 장면의 색깔은 spherical harmonics, 구면 조화 함수로 설계된다는 뜻입니다.
좀 더 읽어보면, 3DGS 과정은 각 3D Gaussian의 위치 (mean), 크기와 방향 (covariance), 투명도 (opacity) 뿐만 아니라, 색깔 (color) 까지 최적화 한다고 합니다. 즉, 더 정확히 말해보자면, 3D Gaussian의 색깔이 구면 조화 함수로 설계되기 때문에 결과 radiance field의 색깔 또한 구면 조화 함수로 표현되었다는 것입니다.
구면 조화 함수는 보통 양자역학과 전자기학에서 구면 대칭인 계를 다룰 때 사용합니다. (저도 학부 때 배운 기억이 있네요) 지금 다루는 컴퓨터 그래픽스 분야에서는 구면 조화 함수가 빛의 반사나 색깔을 표현할 때 쓰인다고 합니다. 왜 구면 조화 함수가 색상 표현에 사용되는지 알아보겠습니다.
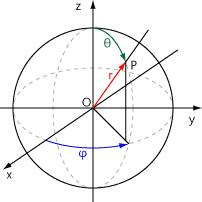
구면 조화 함수는 구의 표면에서 정의되는 함수로, 위 그림과 같은 구면 좌표계에서 특정 위치의 값을 나타냅니다. 거리 (r) 를 제외하고, 각도 (θ: 극각 (polar angle), φ: 방위각 (azimuthal angle)) 를 입력으로 받아, 구 표면의 위치 (P) 에 해당하는 값을 출력하는 방식으로 작동합니다. 일반적인 구면 조화 함수는 다음과 같이 정의됩니다:

위 수식에서 중요한 건 함수 Y(θ, φ)가 l, m 이라는 두 정수, 즉 degree (= l) 와 order (= m) 에 의해 결정된다는 점입니다.
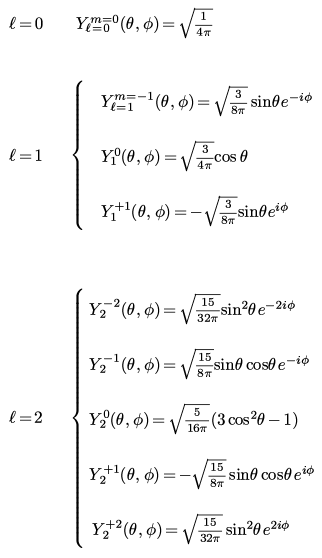
즉, 위 수식처럼 (l,m) = (0,0), (1,-1), (1,0), (1,1), (2,-2), (2,-1), (2,0), ... 에 따라 θ, φ 에 대한 함수가 정해집니다.
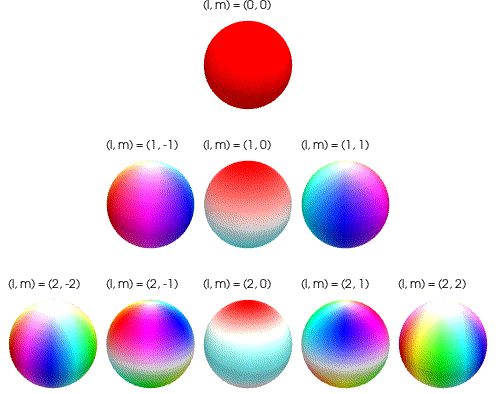
이때 이 구면 조화 함수를 서로 다른 degree l에 대해 시각화하면 위 그림과 같습니다. 구의 표면에 다양한 intensity와 direction을 가지는 색상 패턴으로 표현됩니다. 위 그림은 degree l = 2 까지만을 나타냅니다.
이것을 구면 조화 함수의 degree와 order에 따른 color basis 라고 합니다. 우리는 이제 이 구 형태의 기본 단위들을 여러 조합으로 섞어서, 우리가 원하는 색깔을 만들 수 있습니다.
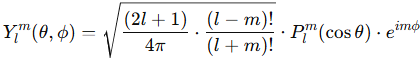
다시 수식으로 돌아와보겠습니다. 지금까지 정리한 내용을 통해, 우리는 위 구면 조화 함수 Y에서 degree l, order m 값이 정해지면, view가 변화할 때마다 바뀌는 θ, φ 에 따른 색상값을 color basis로써 손쉽게 표현할 수 있다는 것을 알았습니다. 이제 이 color basis들을 weighted sum 형태로 섞어서, 3D Gaussian 하나의 색상을 정할 수 있습니다.
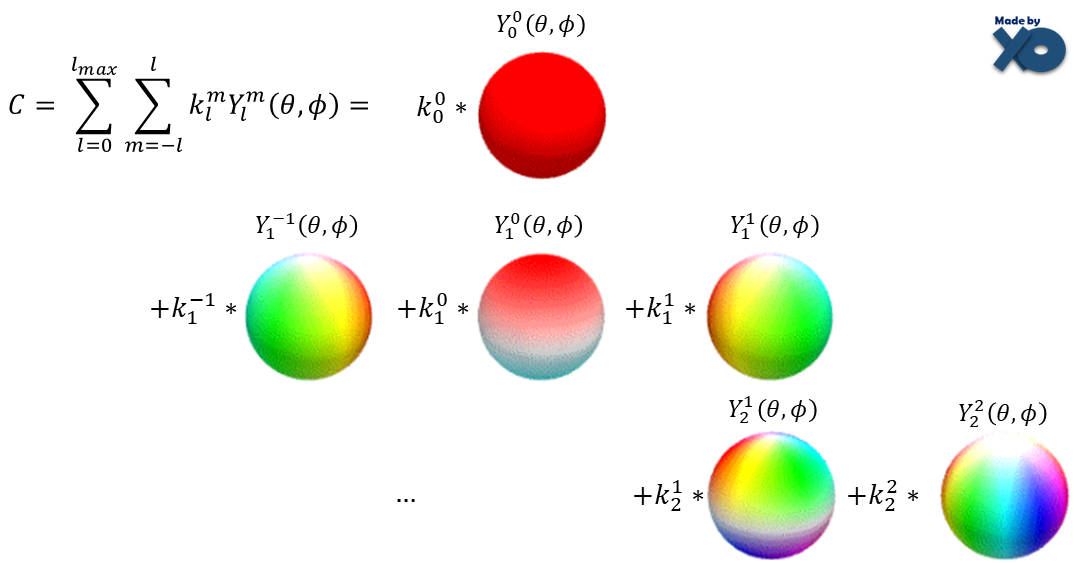
Color 값 C는 구면 조화 함수 Y에 대한 가중치 k의 weighted sum으로 계산됩니다. 비유하자면, Y는 색상 팔레트를 나타내며, 각 팔레트의 색상은 고유의 가중치 값 k를 가집니다. 특정 입력 각도 θ, φ 에 따라 Y는 각각 다른 색상 값을 반환하며, 이 값들은 각 가중치에 의해 조합되어 최종적으로 하나의 색상이 생성되고, 이것이 곧 3D Gaussian 1개의 색상이 됩니다.
쉬운 설명을 위해 k를 가중치라고 했지만, 사실 이것이 SH coeffiecient 입니다. 처음에, 3DGS 과정이 3D Gaussian의 mean, covariance, opacity 뿐만 아니라 color도 최적화한다고 했습니다. 이때 그 color라는 것이 바로 SH coeffiecient 입니다. 3DGS는 3D 장면의 완벽한 view-dependent appearance을 위해 SH coeffiecient를 최적화합니다.
결론적으로, 3DGS 과정에서는 하나의 3D Gaussian의 색상을 표현하기 위해 여러 l, m에 따른 color basis의 weighted sum을 사용하고, 렌더링을 통해 radiance field를 2D 장면으로 만들기 위해선 그렇게 생성된 3D Gaussian들의 조합을 투명도 (opacity) 와 함께 사용합니다. 렌더링 과정은 뒤에서 수식과 함께 더 자세히 설명하겠습니다.
4. Opacity (A, α) : 3D Gaussian의 투명도 (밀도) 결정
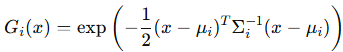
다시 3D Gaussian의 수식으로 돌아오겠습니다. Rasterization 과정에서의 blending 시, 투명도 α 값이 각 projection 된 2D Gaussian에 곱해져, 포인트들로부터 생성된 각각의 2D Gaussian의 투명도가 결정됩니다. 코드에 정의된 투명도 값은 단일 실수 값이며, 최종적으로 0~1 사이 값으로 최적화됩니다.
즉, 서로 다른 투명도를 가진 3D Gaussian들 (다양한 색상, 크기, 위치와 방향 또한 가짐) 을 겹쳐서 3D 장면을 표현하는 radiance field를 생성하고, 3D Gaussian들을 2D 평면에 projection 시켜 2D Gaussian으로 만든 후, 이를 바탕으로 Novel-view synthesis, 즉 다양한 시점에서 2D 이미지를 렌더링하는 것입니다. 뒤에서 더 자세히 설명해보겠습니다.
3DGS Process: Optimization - Overview

3DGS의 과정 중 Initalization 단계가 드디어 끝났습니다. 관련 개념들을 처음 정의하느라 글의 내용이 많이 길어졌습니다. 사실 논문에 나와있는 pseudo code 상, Initalization 단계도 Optimization 단계이지만, 편의상 나눴습니다.
이제 3DGS의 과정 중 학습 단계라고 할 수 있는 Optimization 단계를 설명해보겠습니다.
1. GT (Ground Truth) 이미지 I_hat과, 해당 이미지를 촬영한 카메라의 위치 정보인, 카메라 포즈 V를 가져옵니다. 여기서 카메라 포즈는 위의 SfM 알고리즘 설명에서 언급한 카메라의 Extrinsic parameter와 동일한 단어입니다. 즉, 카메라 포즈는 3D 공간에서 카메라가 어디에 위치하고, 어디를 바라보는지를 나타냅니다.
2. Initialization 단계에서 정의된 M (평균) , S (공분산) , C (색깔) , A (투명도) 와, 1번에서 가져온 카메라 포즈 V를 바탕으로, 3D Gaussian들을 만들고 이를 Rasterize 하여 2D 이미지로 I로 만듭니다. 구체적인 Rasterization 과정은 잠시 후 살펴보도록 하겠습니다.
3. 3DGS 과정을 통해 렌더링된, 다시 말해 예측된 이미지인 I와, GT 이미지 I_hat 사이의 Loss를 측정하고, 이에 따른 Gradient를 측정합니다. Loss는 아래 수식과 같이 L1 loss와 D-SSIM loss의 가중합을 사용하며, λ = 0.2를 사용합니다.
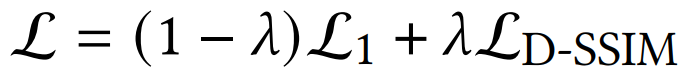
- L1 loss는 픽셀 단위의 정확도를 보장하여 정량적 품질을 높이는 데 유리합니다.
- D-SSIM loss는 이미지의 구조적 정보를 보존하여 시각적 품질을 높이는 데 유리합니다.
- 두 Loss의 조합은 복원된 이미지가 정량적, 시각적 측면에서 모두 우수한 품질을 갖도록 합니다.
4. 3번에서 계산된 Loss에 대한 gradient를 Adam optimizer로 최적화합니다. 이 과정에서 GT 이미지 I_hat과 예측된 이미지 I 사이의 차이를 줄이는 3D Gaussian의 파라미터 M, S, C, A를 찾아나갑니다.
즉, 최적화가 완료되면 최적의 파라미터 M, S, C, A로 이루어진 3D Gaussian들이 만들어지고, Radiance Field는 이들을 기반으로 구성됩니다. 즉, 최적화가 완료된 3D Gaussian들의 뭉치 = Radiance Field라고 쉽게 생각해 볼 수 있습니다. 이 Radiance Field를 가지고, novel-view (새로운 시점) 의 장면을 2D로 렌더링 할 수 있게 됩니다.
3DGS Process: Optimization - Rasterization
Optimization 단계 중 두 번째에 수행되는 Rasterization에 대해 설명하겠습니다.
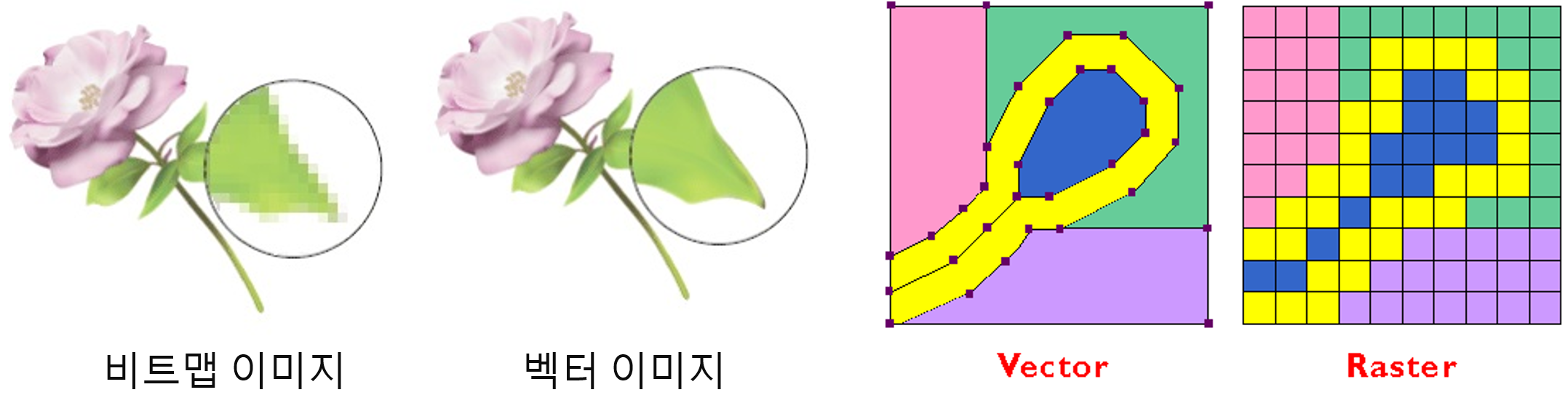
Rasterization의 본래 정의는 벡터 이미지를 래스터 (= 비트맵) 이미지로 변환하는 작업을 뜻합니다.
3DGS에서의 Rasterization이란, 3D Gaussian으로 구성된 Radiance Field를 특정 카메라 포즈에서 봤을 때, 그때 보이는 2D 이미지를 렌더링하는 방법입니다.
논문에서 제안하는 Tile-based Rasterizer는 2D 이미지 공간에서 Gaussian을 타일 단위로 사전 정렬하여, 기존의 픽셀 단위 정렬 방식에서 발생했던 높은 계산 비용을 피하도록 설계되었습니다. 이를 통해 효율적인 α-blending을 구현할 수 있었고, 결과적으로 빠른 렌더링이 가능해졌습니다. 또한, 여러 2D Gaussian이 혼합된 경우에도 효율적인 back-propagation을 지원하며, 처리할 수 있는 2D Gaussian의 개수에 제한이 없습니다. 이 과정은 메모리 사용량이 낮아 효율적입니다.
추가적으로, 이 Rasterization 파이프라인은 완전 미분 가능 (differentiable) 하도록 설계되어, Rasterization 결과로 생성된 이미지를 loss 함수에 입력하고, 미분을 통해 다음 iteration에서 2D 공간으로 projection 될 3D Gaussian의 위치(M), 공분산(S), 색상(C), 투명도(A) 를 최적화할 수 있습니다.
왜 그런 것인지, 3DGS에서의 Rasterization을 pseudo code와 함께 단계별로 분석하며 알아보겠습니다.

먼저 입력으로는 rasterize 할 해당 이미지의 가로 길이 w와 세로 길이 h, 3D Gaussian의 평균, 공분산, 색깔, 투명도인 M, S, C, A, 그리고 해당 이미지를 촬영한 카메라 포즈 V를 가져옵니다. Rasterization이 Optimization의 한 과정이므로, 입력값은 Optimization의 것을 그대로 따릅니다.
1. CullGaussian
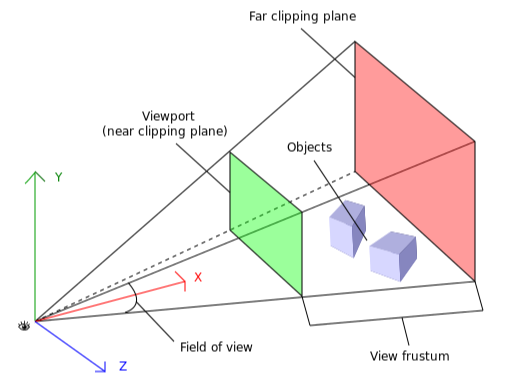
먼저, 절두체라고 해석되는 view frustum에 대해, 3D Gaussian을 걸러내는 (culling) 과정으로 시작합니다. 구체적으로, 99% 신뢰도로 view frustum과 교차하는 3D Gaussian만 유지합니다. 쉽게 말하면, 주어진 카메라 포즈 V의 뷰에서 관측될 수 있는 유효한 3D Gaussian만 남기고, 나머지 3D Gaussian은 제거한다고 볼 수 있습니다.
추가적으로, 극단적인 위치에 있는 3D Gaussian은 (예: 평균이 near/far plane에 매우 가깝거나 view frustum 바깥으로 크게 벗어난 경우) guard band를 사용해 간단히 제외합니다. 이는 해당 3D Gaussian의 projection 된 2D 공분산을 계산할 때 발생할 수 있는 불안정성을 방지하기 위함입니다.
2. ScreenSpaceGaussian
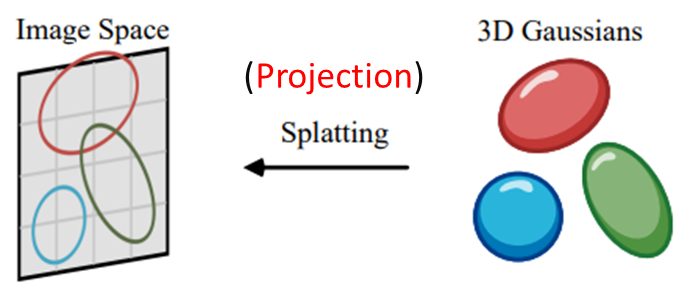
ScreenSpaceGaussian에서는 3D Gaussian을 2D 평면 (2D 이미지 공간) 에 projection 하여 2D Gaussian으로 만들어줍니다. 해당 projection 과정은 3D Gaussian의 3x3 공분산 행렬 Σ를 2x2 공분산 행렬 Σ'으로 바꿔줌으로써 일어납니다.
위 그림은 3DGS survey 논문에서 가지고 온 것인데, 해당 논문에선 Splatting을 projection과 동일하게 보고 있습니다. 제가 추가적으로 단어 Splatting 위에 Projection을 추가했습니다. (뒤의 그림들도 3DGS survey 논문에서 가져왔습니다)
Zwicker [2001a] 등에 따라, 2D 이미지 평면으로 projection 된 3D Gaussian의 공분산 Σ'는 3x3 행렬 대신에 2x2 행렬로 표현할 수 있다고 Initialization 단계에서 설명했습니다. 즉, Σ'를 통해 3차원의 3D Gaussian을 2차원의 2D Gaussian으로 변환한 것입니다.
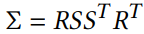
Initialization 단계에서 설명하였듯, 3D Gaussian의 공분산 Σ은 위와 같고, 3D 행렬입니다.
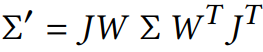
Σ를 2D 이미지 평면으로 projection 하여 Σ'로 만드는 과정도 Initialization 단계에서 위 수식으로 설명했습니다.
3. CreateTiles
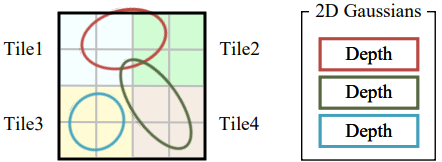
2D 평면에 3D Gaussian들이 projection 되어 2D Gaussian이 되었습니다. 이제 이 2D Gaussian들을 포함하고 있는 2D 평면을, 하나당 16x16 픽셀 크기를 가진 타일로 나눠줍니다. 이 타일은 3DGS survey 논문에선 non-overlapping patch라고 표현하기도 합니다. 그림은 타일 하나당 2x2 픽셀을 가진 것으로 표현되어 있는데, 실제론 16x16 픽셀입니다.
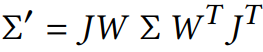
각 2D Gaussian에는 깊이 값인 depth가 부여되며, 이 depth는 카메라로부터 해당 3D Gaussian까지의 거리를 나타냅니다. 예를 들어, 3D Gaussian이 카메라에 가까울수록 작은 depth 값을 가지며, 멀수록 큰 depth 값을 가집니다. 이 depth 값은 관점 변환 (viewing transformation) 행렬 W를 통해 계산할 수 있습니다.
3D Gaussian의 원래 좌표는 월드 좌표계에 정의되어 있습니다. 하지만 렌더링은 카메라 좌표계를 기준으로 이루어지므로, 3D Gaussian의 위치를 카메라 기준으로 변환해야 합니다. W는 월드 좌표계를 카메라 좌표계로 변환하는 행렬로, 이를 통해 3D Gaussian의 위치를 카메라 좌표계로 변환할 수 있습니다. 변환된 카메라 좌표계에서 축 값을 읽으면 해당 3D Gaussian의 depth 값을 얻을 수 있습니다.
이렇게 계산된 각 3D Gaussian의 depth는 투영된 2D Gaussian에 부여되며, 이 depth 값을 기준으로 2D Gaussian을 정렬합니다. 이후 그렇게 정렬된 순서로, 픽셀 단위에서 2D Gaussian을 α-blending 합니다. 뒤의 BlendInOrder 단계에서 이 과정에 대해 더 자세히 설명하겠습니다.
참고로, 논문의 Chapter 6에 따르면 Tile-based Rasterization은 먼저 screen을 16x16 타일로 분할한 뒤, view frustum과 각 타일에 대해 3D Gaussian을 culling 하는 과정으로 시작한다고 되어있습니다. 그러나 Appendix의 pseudo code (현재 설명 중인) 는 3D Gaussian을 culling 하고 → 2D 평면에 3D Gaussian을 projection 한 뒤에 → 그 2D 평면을 타일로 분할한다고 되어있습니다. 즉 culling이 먼저냐 타일 분할이 먼저냐의 차이인데, 우선 이 게시물에선 Appendix의 pseudo code 순서를 따라 설명하고 있습니다.
4. DuplicateWithKeys
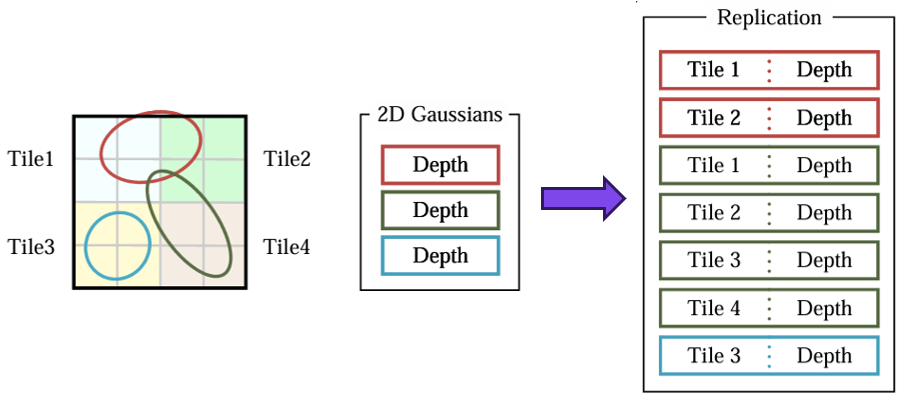
각 2D Gaussian이 차지하는 타일 수 만큼 해당 2D Gaussian을 복제합니다. 이것을 각 2D Gaussian들을 instance화 한다고 합니다. 각 instance들은 총 64bits 길이의 dictionary key로 설계됩니다. 이때 key의 lower 32bits는 이전 단계에서 구한 3D Gaussian의 depth 값 (즉, projected depth) 으로 인코딩되고, higher 32bits는 2D Gaussian이 차지하는 타일의 인덱스로 인코딩 됩니다. 타일 인덱스의 정확한 크기는 현재 해상도에서 갖는 16x16 타일의 수에 따라 달라집니다.
예시 그림을 통해 2D Gaussian이 몇 개나 복제되는지 살펴보겠습니다. (그림의 Replication) 빨간색 2D Gaussian은 Tile1과 Tile2를 차지하고 있으므로 2개, 초록색 2D Gaussian은 Tile1, Tile2, Tile3, Tile4를 차지하고 있으므로 4개가 복제되며, 파란색 2D Gaussian은 Tile1만 차지하고 있으므로 1개가 그대로 유지됩니다.
5. SortByKeys
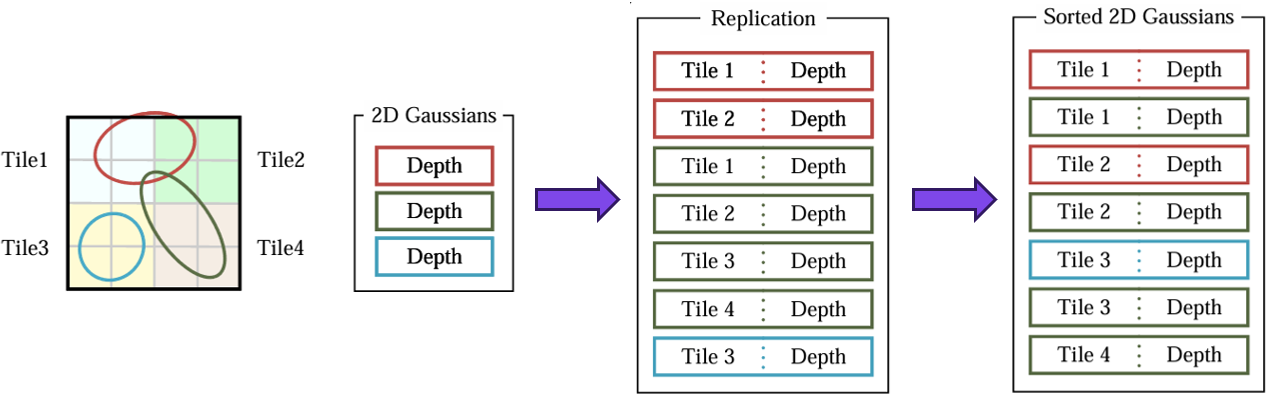
이전 단계에서 설계된 key를 바탕으로, Single Fast GPU Radix Sort (기수 정렬 : 낮은 자리수부터 비교하여 정렬) 를 통해, 복제된 2D Gaussian들을 정렬합니다. 해당 과정을 Depth ordering이라고 하며, 각각의 타일에 존재하는 모든 splat에 대해 병렬적으로 수행됩니다.
각 픽셀에 대해선 추가적인 ordering 없이, depth에 대해서만 수행된 ordering을 기반으로 이후 blending이 실행됩니다. 이를 통해, blending이 실행되는 BlendInOrder 단계에서, key를 기준으로 카메라와 가까운 (= depth가 작은) 2D Gaussian을 먼저 고려할 수 있습니다.
참고로 저는 위 그림을 보고 각 타일을 차지하는 영역이 클수록 Depth가 커지기 때문에, 그림의 Sorted 2D Gaussians의 결과가 저렇게 된 것인가 의문이었습니다. 예를 들어, "Tile1에서는 빨간색 2D Gaussian이 초록색 2D Gaussian 보다 차지하는 영역이 많기 때문에 Tile1에서는 빨간 것이 초록 것보다 앞으로 간건가?" 라고 생각했습니다.
하지만 그런 것은 아니고, 그냥 그림이 착각하기 쉽도록 그려진 것 같습니다. 그림에 있는 각각의 2D Gaussian에는, Sorted된 결과처럼 보일 수 있도록 이전 단계에서 depth가 인코딩 되어있는 것이라 생각하면 되겠습니다. (e.g. Tile1에 대해서, 빨간색 2D Gaussian의 depth = 30, 초록색 2D Gaussian의 depth = 50)
6. IdentifyTileRanges
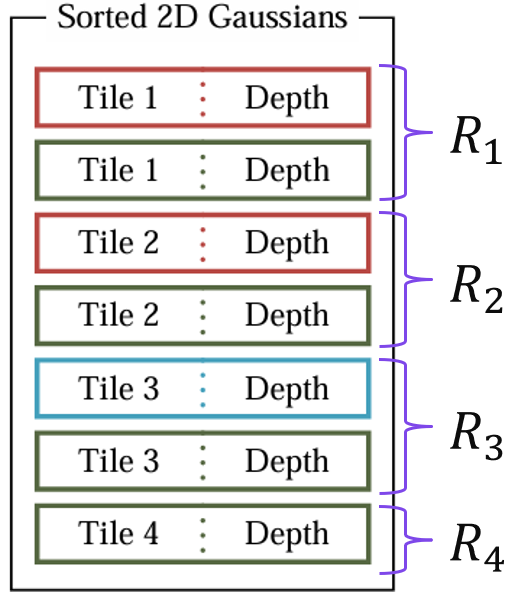
Sorted된 결과에서, 같은 타일 ID를 가진 2D Gaussian들 중 시작과 끝 2D Gaussian을 식별 (identify) 하여, 타일 별 2D Gaussian 리스트 R을 효율적으로 생성합니다. 시작과 끝 2D Gaussian을 정하는 기준은 depth 입니다. 그림으로 설명하자면, Tile1 리스트 R1 = [빨간색, 초록색], Tile2 리스트 R2 = [빨간색, 초록색], Tile3 리스트 R3 = [파란색, 초록색], Tile4 리스트 R4 = [초록색]이 되겠습니다.
이는 병렬적으로 수행되며, 64-bit array element (= 타일 ID와 Depth로 구성된 64bits 길이의 dictionary key) 당 하나의 thread를 실행하여, higher 32 bits ( = 타일 ID) 를 두 개의 neighbor와 비교하는 방식으로 처리됩니다.
이후 Init Canvas 단계를 통해, 공백의 이미지를 생성하여 2D Gaussian들의 α-blending을 준비합니다.
7. GetTileRange
특정 타일 t에 대해서, 해당 타일에 있는 2D Gaussian들을 정렬한 리스트 R (전 단계에서 생성함) 로부터, 범위 값 r을 불러옵니다. 예를 들어 특정 타일 t = Tile1에 대한 리스트 R = [빨간색, 초록색]에서는 리스트의 요소가 2개이므로, r = 2가 될 것입니다. (논문에 이 과정에 대한 정확한 정보는 없어서, 제가 추측해본 동작 방식입니다)
8. BlendInOrder
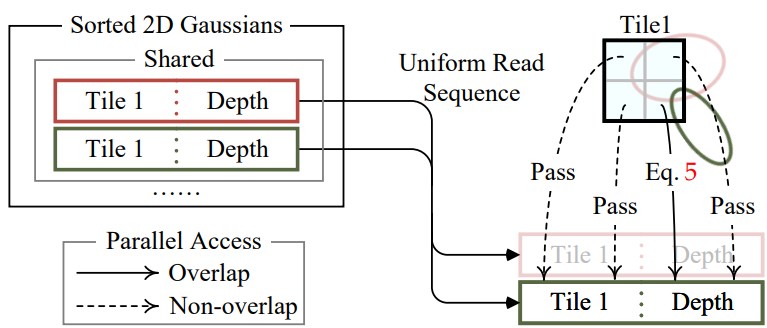
2D Gaussian을 순서에 따라 섞는 과정인 BlendInOrder 과정은, 각 타일마다 하나의 Thread block으로 실행됩니다. 각 block은 먼저 shared memory에 Gaussian들을 로드한 후, 각 픽셀에 대해 Gaussian 리스트를 앞에서부터 순차적으로 탐색하면서 2D Gaussian의 색상과 투명도 값을 누적합니다. (그림의 Eq.5는 Point-based alpha blending 수식으로, 바로 아래에서 설명합니다)
이때 타일 내 렌더링은 Gaussian 리스트를 한 번만 순회(iterate)하면 완료될 수 있습니다. 이를 통해 데이터 로딩/공유/처리 과정에서 병렬성을 극대화할 수 있습니다.
각 픽셀에서 목표 투명도 (즉, saturation) 에 도달하면 해당 thread는 중단됩니다. 또한, 일정 간격마다 타일 내의 threads 상태를 확인하며, 타일 내 모든 픽셀이 목표 투명도에 도달하면 해당 타일의 처리를 종료합니다.
즉, BlendInOrder는 각 타일에 배치되어 있는 2D Gaussian의 색상과 투명도를 누적하여, novel-view synthesis 하고자 하는 장면(scene)의 픽셀값을 결정하는 과정이라 할 수 있습니다.
이번 과정을 수식과 함께 좀 더 알아보겠습니다. 구체적으로, 이러한 방식을 Point-based alpha blending이라고 합니다.
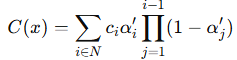
여기서 C(x)는 N개의 2D Gaussian 색상 c와 최종 투명도 α'를 누적하여 생성 (= 렌더링) 한, 픽셀 x의 최종 색상을 의미합니다. 이때 최종 투명도 α'는 2D Gaussian G'(x)와 그것의 자체 투명도 α의 곱을 통해, 다음과 같이 표현됩니다.
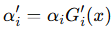
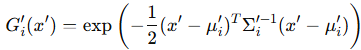
다시 한번 설명하자면, 2D Gaussian G'(x)에서, x'과 µ'은 projected space의 x와 µ를 의미합니다. 이때 3DGS survey 논문을 따라, 수식에서 최종 투명도를 α', 2D Gaussian 자체의 투명도를 α로 쓰고 있는데, 헷갈리지 않으시길 바랍니다.
즉, point-based alpha blending은 카메라 중심 근처에 있는 3D Gaussians의 기여도를 강조하고, 먼 거리에 있는 3D Gaussians의 기여도는 지수적으로 감소시키도록 설계되었습니다.
참고로, NeRF에서도 ray marching이라는 기법을 통해 하나의 픽셀값을 생성합니다. 도입부에서도 간단히 설명하긴 했지만, 말이 나온 김에 NeRF와 3DGS가 픽셀값을 생성하는 방식의 공통점과 차이점을 더 자세히 한 번 더 알아보겠습니다.
공통점
- Alpha Blending을 사용한 색상 합성
- NeRF에서는 ray-marching을 수행하면서 투명도(α) 기반 누적 합산을 통해 최종 색상을 결정.
- 3DGS에서도 point-based alpha blending을 사용하여 Gaussian을 중첩하며 최종 색상을 결정.
- 즉, 두 방법 모두 "가까운 객체가 더 강한 영향을 주도록 하는" alpha-weighted blending을 수행.
- 3D 공간의 표현을 2D 이미지로 투영하여 최종 렌더링
- NeRF는 volume rendering을 사용하여, ray를 통해 샘플링한 3D 공간의 정보를 모아 2D 이미지 생성.
- 3DGS는 Gaussian Splatting을 통해 3D Gaussian을 2D 픽셀 공간으로 projection하여 색상을 합성.
- 결국, 둘 다 3D 정보를 2D로 변환하는 렌더링 방식을 사용.
- Depth 정보를 활용한 정렬 기반 합성
- NeRF는 ray를 따라 depth 순서대로 샘플링된 값을 앞에서부터 누적하여 최종 색상 계산.
- 3DGS의 point-based alpha blending도 Gaussian을 depth 순서대로 정렬 후 누적해 렌더링.
- 즉, 둘 다 depth-aware blending 방식을 활용.
차이점
- NeRF는 Ray Marching, 3DGS는 Point-based Splatting
- NeRF는 ray를 따라 샘플을 일정 간격으로 쌓으며 볼륨 렌더링을 수행.
- 3DGS는 3D 공간 내 개별적인 Gaussian을 2D 픽셀 공간으로 직접 투영 후 blending.
- NeRF는 연속적인 샘플링, 3DGS는 이산적인 Gaussian 샘플링
- NeRF는 연속적인 공간에서 ray를 따라 일정 간격으로 샘플링.
- 3DGS는 이산적인 Gaussian 분포를 기반으로 샘플링하여 렌더링.
- NeRF는 Ray를 따라 1D 정렬, 3DGS는 2D Projection 기반
- NeRF는 특정 픽셀에서 오직 한 개의 ray만 샘플링하여 정렬된 값을 blending.
- 3DGS는 동일한 픽셀에 영향을 주는 여러 Gaussian들을 2D 공간에서 depth 기준으로 정렬 후 blending.
정리하자면, Rasterization은 3D Gaussian을 중첩하여 novel-view에서 하나의 픽셀을 생성하는 과정입니다. 이를 위해 3D Gaussian을 projection하여 2D Gaussian으로 변환한 후, 그처럼 특정 색상과 투명도를 가진 2D Gaussian들을 순차적으로 누적하여 최종적인 픽셀 값을 구성합니다.
3DGS Process: Optimization - Adaptive Density Control
Rasterization이 이번 3DGS의 핵심이라고 생각해, 자세히 설명을 해보았습니다. 이제 Optimization의 마지막 단계인 Adaptive Density Control을 알아보고 3DGS Process 파트 설명을 마치겠습니다.

이 부분은 생성할 장면에 맞게 3D Gaussian 들의 갯수를 조절하는 과정으로 이루어져 있습니다. M, S, C, A는 매 iteration마다 업데이트되지만, 해당 과정은 100 iteration마다 수행됩니다. 즉, 지금까지 설명한 Rasterization 과정을 통해 픽셀 생성을 거쳐 렌더링 된 장면 I과, 정답값 장면 I_hat 간의 차이를 줄이는 최적화된 M (평균) , S (공분산) , C (색깔) , A (투명도) 는 계속 찾아나가되, 잠깐잠깐 3D Gaussian 들의 갯수도 조절한다고 생각하면 됩니다.
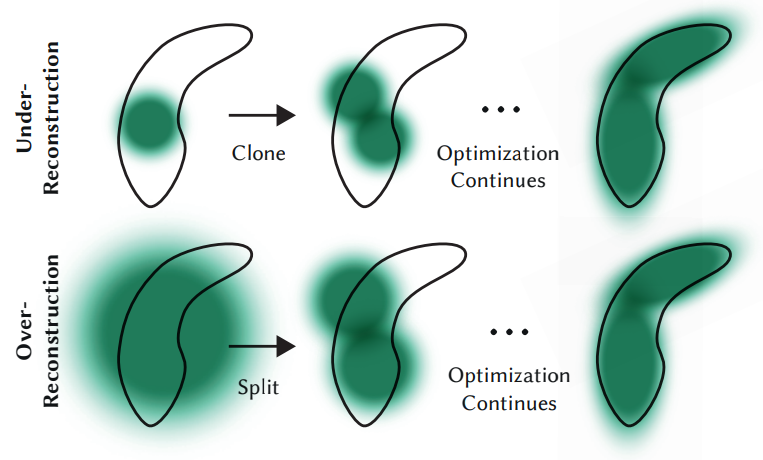
3D Gaussian이 경우에 따라 Remove / Clone / Split 합니다. 하나씩 살펴보겠습니다.
Remove
특정 threshold보다 낮은 투명도(A)를 가졌거나, 크기(S)가 너무 큰 3D Gaussian을 제거합니다. 이후 Under-Reconstruction 되어 기하학적 특징을 파악하지 못한 영역에 대해선 3D Gaussian을 Clone 해서 처리하고, Over-Reconstruction 되어 넓은 영역을 지나치게 모델링한 3D Gaussian들은 Split 해서 처리합니다.
3D Gaussian을 Clone 또는 Split하는 과정을 Densification이라고 하는데, 이 과정은 positional gradient인 ∇𝑝L이 특정 threshold τ_p를 넘으면 이루어집니다.
positional gradient ∇𝑝L은 말 그대로 position에 대한 loss 변화량인데, 3D Gaussian이 어떤 영역을 너무 많이 or 적게 커버할 때 큰 값을 갖도록 설계되어있습니다. 이는 loss가 작아지는 방향 (= ∇𝑝L이 큰 방향) 으로 3D Gaussian의 위치 (M) 를 옮겨 주어야 하기 때문입니다.
Clone / Split
Clone / Split은 ∇𝑝L > τ_p인 상황에서 이루어집니다.
3D Gaussian의 커버 영역 ||S|| < τ_s : 즉 Under-Reconstruction 일 때, 3D Gaussian을 Clone 합니다. 해당 3D Gaussian과 똑같이 복사하고, 전체 volume도 증가하면서 3D Gaussian의 개수가 증가합니다.
3D Gaussian의 커버 영역 ||S|| > τ_s : 즉 Over-Reconstruction 일 때, 3D Gaussian을 Split 합니다. 3D Gaussian을 쪼갤 때 실험적으로 결정된 값 1.6 scale로 나누며, 전체 volume은 유지되면서 3D Gaussian의 개수가 증가합니다.
Experiments
실험 결과는 핵심적인 부분만 간단하게 짚고 넘어가겠습니다.

3DGS가 NeRF-based 모델들보다 더 우수한 성능으로 novel-view synthesis 하는 것을 확인할 수 있습니다.

3DGS가 NeRF-based 모델들보다 더 우수한/견줄만한 성능을 보이고 있고, 월등히 앞서는 훈련 속도와 실시간 렌더링 속도 (FPS) 를 보이고 있습니다.

Densification (3D Gaussian Clone / Split) 과정을 모두 거쳤을 때 시각적 성능이 향상됨을 알 수 있습니다.
더 다양한 시각적 결과는 3DGS 프로젝트 페이지에서 확인하실 수 있습니다:
https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/
Wrap-Up
지금까지 3DGS에 대해 자세히 알아보았습니다. NeRF 기반의 방법들보다 훨씬 효율적으로 높은 성능을 도출하는 특성 덕분에, 저는 개인적으로 novel-view synthesis를 실생활에 응용할 수 있는 길을 열어주었다고 봅니다. 현재는 3DGS의 한계점을 풀어내는데 성공한 여러 논문들이 있고 계속 발전하는 분야입니다. 대표적으로 다음과 같은 문제들과 이를 해결한 방법들이 있습니다:
1) 부족한 데이터로 인해 렌더링 시 생성되는 artifact 문제 → DNGaussian, PixelSplat
2) large-scale의 장면을 훈련, 렌더링, 저장할 때, 많은 메모리 사용량이 요구되는 문제 → Compact-3DGS, HAC
3) 복잡한 장면이나 다양한 뷰 및 조명 조건에서 기본적 기하학과 구조를 무시하는 문제 → Gaussianpro, 2DGS, SuGar
4) 해상도가 달라질 때 Aliasing (blurring or jagged edges) 에 취약한 문제 → Multi-Scale 3DGS, Analytic-Splatting
5) SfM 기반으로 initialization 할 시 조금만 에러가 나도 성능에 큰 영향을 주는 문제 → COLMAP-Free 3DGS
6) 동적으로 움직이는 물체, 즉 시간적 요소가 포함된 장면을 렌더링 하지 못하는 문제 → 4DGS
또한 3DGS를 다양한 분야에서 응용한 논문들도 많습니다. 이는 아래 그림으로 대체하겠습니다.
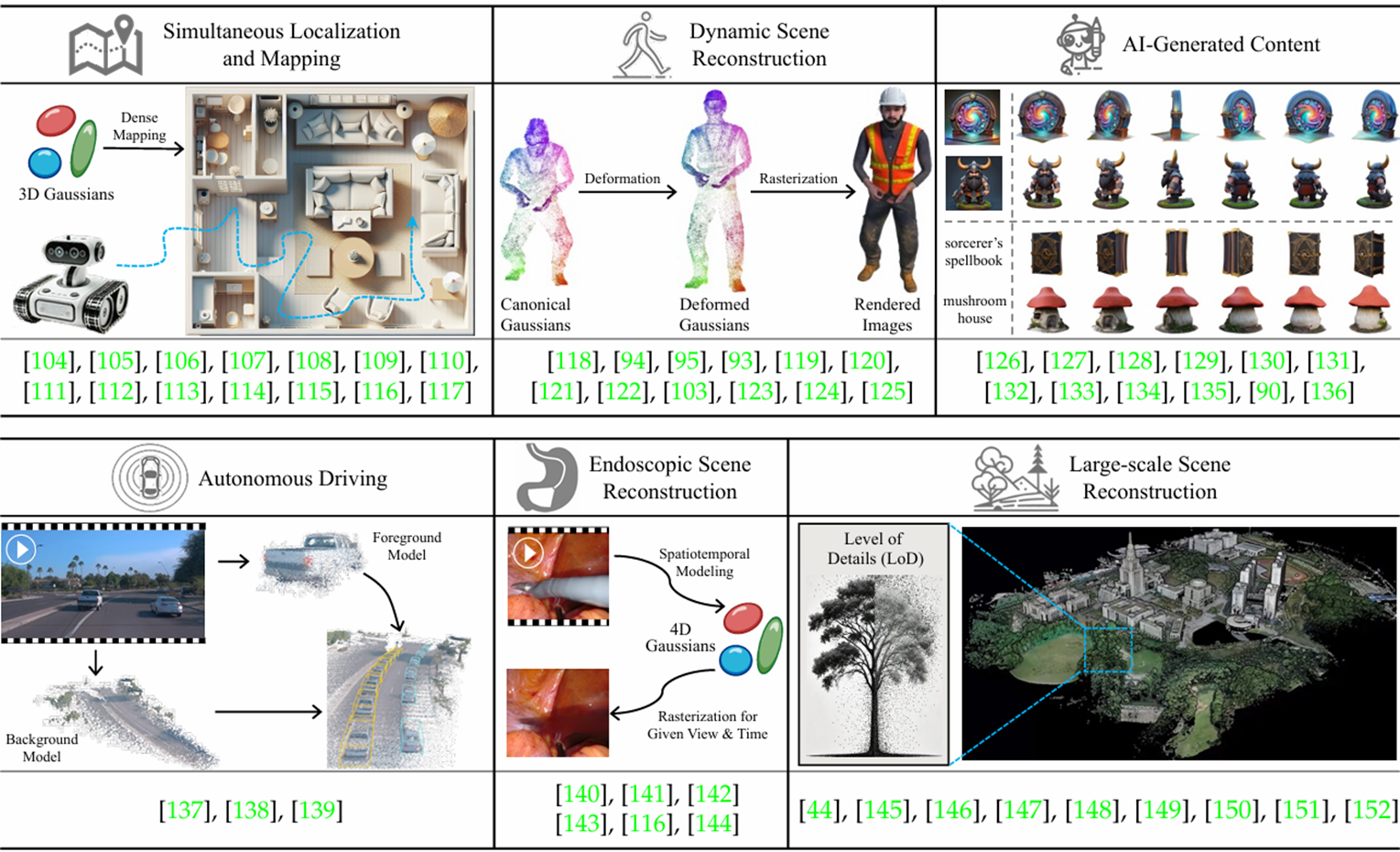
이상으로 앞으로가 더욱 기대되는 3DGS 리뷰를 마칩니다. 긴 글 읽어주셔서 감사합니다.
※ 3DGS를 도커로 빌드한 깃허브와 빌드 과정 포스팅도 있으니, 관심있으시면 방문 부탁드립니다. 다시 한번 감사합니다!
3DGS 도커 빌드 과정: https://mole-starseeker.tistory.com/119
3DGS 도커 빌드 깃허브: https://github.com/jhcha08/3DGS-Docker
GitHub - jhcha08/3DGS-Docker: Dockerized version of the 3D Gaussian Splatting
Dockerized version of the 3D Gaussian Splatting. Contribute to jhcha08/3DGS-Docker development by creating an account on GitHub.
github.com
참고 문헌 및 블로그
https://arxiv.org/abs/2308.04079
3D Gaussian Splatting for Real-Time Radiance Field Rendering
Radiance Field methods have recently revolutionized novel-view synthesis of scenes captured with multiple photos or videos. However, achieving high visual quality still requires neural networks that are costly to train and render, while recent faster metho
arxiv.org
https://arxiv.org/abs/2401.03890
A Survey on 3D Gaussian Splatting
3D Gaussian splatting (GS) has emerged as a transformative technique in explicit radiance field and computer graphics. This innovative approach, characterized by the use of millions of learnable 3D Gaussians, represents a significant departure from mainstr
arxiv.org
[논문 리뷰] 3D Gaussian Splatting (SIGGRAPH 2023) : 랜더링 속도/퀄리티 개선
3D Gaussian Splatting for Real-Time Radiance Field Rendering, Bernhard Kerbl, SIGGRAPH 2023 NeRF분야에서 뜨거운 이슈가 된 논문입니다. NeRF에서 해결하고자 하는 Task와 동일하게, 여러 이미지와 촬영 pose 값이 주어지
xoft.tistory.com
https://happy-support.tistory.com/25
[쉽고 간결한 논문 리뷰] 3D Gaussian Splatting for Real-Time Radiance Field Rendering (SIGGRAPH 2023)
본 논문은 University of Nice Sophia Antipolis와 Max Planck Institute for Informatics에서 2023년에 작성한 논문이다.논문 링크: https://arxiv.org/abs/2308.04079 1. IntroductionNovel view synthesis란?여러 시점에서 촬영된 이미
happy-support.tistory.com
3D Gaussian Splatting for Real-Time Radiance Field Rendering 리뷰
3D Gaussian Splatting 리뷰
velog.io
https://clean-dragon.tistory.com/13
[논문리뷰] 3D Gaussian Splatting
본 포스팅은 논문 3D Gaussian Splatting for real-time radiance field rendering 를 읽고 정리한 내용입니다.아는 것이 많이 없어서 부족한 부분이 많습니다. 혹여나 틀린부분 있다면 지적해주시길 바랍니다!
clean-dragon.tistory.com
https://www.reconlabs.ai/blog/?bmode=view&idx=17059184
[R:세미나] 리콘랩스 오픈 세미나 #3, ‘NeRF & Gaussian Splatting’ : 리콘랩스(RECON Labs)
리콘랩스의 사내 오픈세미나는 어느덧 세 번째 차례를 맞았습니다. “NeRF & Gaussian Splatting” 주제로 세미나가 진행되었어요.사내 오픈 세미나에서는 현재 서비스에 활용되는 기술뿐만이 아니라
www.reconlabs.ai
https://kyujinpy.tistory.com/138
[3D Gaussian Splatting 간단한 논문 리뷰]
*Gaussian Splatting에 대한 간단한 논문 리뷰 입니다!*이해를 돕기 위해 수식은 거의 제외했습니다. GS 논문: repo-sam.inria.fr/fungraph/3d-gaussian-splatting/3d_gaussian_splatting_high.pdf GS github: 3D Gaussian Splatting for
kyujinpy.tistory.com
'딥러닝 & 머신러닝 > 논문 리뷰' 카테고리의 다른 글
| [논문 리뷰] Descanning: From Scanned to the Original Images with a Color Correction Diffusion Model (0) | 2024.12.21 |
|---|---|
| [논문 리뷰] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (0) | 2024.07.28 |
| [논문 리뷰] Super Resolution - RFDN (ECCVW 2020) (0) | 2022.01.02 |
| [논문 리뷰] CNN - RepVGG (CVPR 2021) (0) | 2021.12.28 |
| [논문 리뷰] Super Resolution - MSRN (ECCV 2018) (0) | 2021.07.19 |




